Определение момента инерции параллелепипеда методом крутиль­ных колебаний

1.  Цель работы:определение момента инерции параллелепипеда методом крутиль­ных колебаний.

2. Теоретические основы работы.

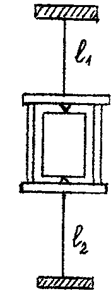Унифилярный подвес (крутильный маятник) предназначен для изучения динамики крутильных колебаний, определения моментов инерции твер­дых тел и упругих характеристик материала при кручении.

Крутильный маятник (рис.1) состоит из рамки, закрепленной на растяжках (тонких упру­гих проволоках). В рамке может быть закреплено твердое тело с центром масс, лежащим на оси вращения. Если повернуть рамку на малый угол j от положения равновесия и отпустить, то она начнет совершать гармонические крутильные колебания.

Движение рамки с телом можно описать, используя основное урав­нение вращательного движения твердого тела в проекции на ось вращения.

М = Je

Рис.1

Здесь J - момент инерции рамки с телом; e - угловое ускорение;

M - момент сил, действующих на рамку, при ее вращении относи­тельно неподвижной оси.

Положим, что сопротивление воздуха при движении рамки мало. Тогда на рамку действуют только моменты упругих сил со стороны растяжек l₁ и l₂. Основное уравнение вращательного движения в этом случае имеет вид

Jd²j/dt² = M   (1)

Здесь e = d²j/dt². Отметим, что возникающие при вращении моменты упругих сил таковы, что их действие ведет к уменьшению угла j.

Для линейно упругого тела момент сил упругости при малых деформациях кручения можно записать в виде

М = -kj   (2)

Здесь k - постоянная для данной проволоки величина, называемая модулем кручения. Знак "минус" показывает, что моменты сил упру­гости препятствуют повороту рамки из положения равновесия. Модуль кручения зависит от материала проволоки, от ее геометричес­ких размеров.

Подставим (2) в (1), получим

Jd²j/dt² + kj = 0   (3)

Уравнение (3) - дифференциальное уравнение гармонических кру­тильных колебаний. Его можно записать в виде

Jd²j/dt² + w₀²j = 0   (4),

Где w₀² = k/J

Решением уравнения (4) является

j = j₀cosw₀t

Таким образом, w₀ - циклическая частота колебаний, связанная с периодом колебаний соотношением w₀ =2p/T. Отсюда для периода гармонических крутильных колебаний получаем соотношение

T = 2pÖJ/k   (5)

Согласно (5) период колебаний пустой рамки с моментом инерции J₀ равен Т₀, момент инерции рамки с закрепленным в ней паралле­лепипедом равен J₁, соответствующий период крутильных колебаний равен Т₁. Из (5) имеем

J₀ = kT₀²/4p²   (6)

J₁ = kT₁²/4p²   (7)

Момент инерции параллелепипеда J_эксп. определим, вычитая (6) из (7):

J_эксп.= J₁ – J₀ = (T₁² – T₀²)k/4p²   (8)

Исследуемое тело имеет правильную геометрическую форму: оно представляет собой однородный прямоугольный параллелепипед с массой m, и ребрами а, b и с. Момент инерции параллелепипеда, закреп­ленного так, что одна из граней (со сторонами а и b) перпендику­лярна оси вращения, проходящей через центр масс, может быть рассчи­тан по формуле

J_теор. = m*(a² + b²)/12   (9)

Значения J_эксп. и  J_теор., сравниваются между собой.

3. Описание экспериментальной установки.

Схема экспериментальной установки пред­ставлена на рис.2. На вертикальной стойке 1 закреплены верхний 2, нижний 3 и средний 4 кронштейны. Между кронштейнами 2 и 3 на тонких проволоках 5 как на растяжках закреплена рамка 6, исследуемое тело 7 фикси­руется внутри рамки с помощью специальных зажимов. На среднем кронштейне 4 размещена шкала 8, электромагнит, фиксирующий рамку в заданном начальном положении, а также фотоэлектрический датчик 9, предназначен­ный для отсчета времени и числа периодов колебаний. Флажок, установленный на рамке, пересекает световой поток от лампочки к фотодатчику. При этом сигнал с фотодатчика поступает на секундомер 10 с цифровой индикацией, начинается счет времени и чис­ла периодов колебаний. Счет времени и периодов прекращается после нажатия кла­виши "Стоп" секундомера и последующего пересечения флажком светового потока. Вклю­чение установки осуществляется нажатием клавиши "Сеть" секундомера, а запуск системы - нажатием клавиши "Пуск". Предварительно показания времени и периодов устанавливаются на нуль, нажатием клавиши "Сброс". Следует помнить, что, если необходимо измерить время N полных коле­баний, то остановка счета производится нажатием клавиши "Стоп" в тот момент, когда табло "периоды" показывает число N – 1.