



ЗАДАНИЕ 1. АЛГЕБРОИЧЕСКИЕ И ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ.
В теории автоматического регулирования обоснован ряд критериев—признаков устойчивости линейных АСР.
Критерии устойчивости представляют собой правила, устанавливающие устойчивость системы и выявляющие влияние тех или иных параметров и структурных изменений в системе на устойчивость.
Критерии-устойчивости можно разделить на алгебраические и частотные. Алгебраические критерии позволяют определять устойчивость путем выполнения алгебраических операций над коэффициентами исходного дифференциального уравнения системы, не прибегая к графическим построениям. Алгебраические критерии устойчивости отличаются значительной сложностью.
Частотные критерии устойчивости имеют более явный физический смысл. Они позволяют сравнительно просто оценить устойчивость системы и влияние параметров отдельных ее элементов на устойчивость.
Частотные критерии устойчивости, основанные на использовании частотных характеристик, относятся к графо-аналитическим, так как устойчивость оценивают по виду годографа частотой характеристики. Достоинством этого метода является его наглядность и возможность экспериментального определения частотных характеристик как отдельных звеньев, так и системы
в целом.
Алгебраические критерии Рауса и Гурвица устанавливают условие устойчивости на базе определенных комбинаций, составленных из коэффициентов характеристических уравнений вида
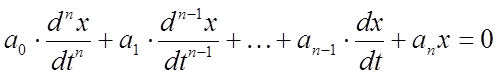 (1)
(1)
и
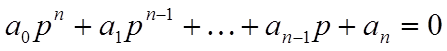 (2)
(2)
Критерий Рауса. Для определения устойчивости линейной АСР по критерию Рауса составляется таблица Рауса. Коэффициенты таблицы называются элементами Рауса. Обозначают каждый элемент через bre , где r — номер строки таблицы Рауса; e — номер столбца. Тогда правила заполнения таблицы Рауса сводятся к следующему.
Элементами первой строки таблицы Рауса являются коэффициенты характеристического уравнения ( 2 ) с четными индексами, т. е. b11 = a0 , b12=a2 b и т. д.
Элементами второй строки таблицы Рауса являются коэффициенты характеристического уравнения ( 2 ) с нечетными индексами, т. е. b21=a1, b22=a3. Элементы остальных строк таблицы определяются на основании общего выражения
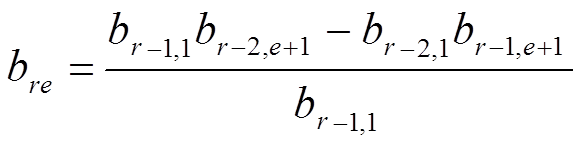
Критерий Рауса, исходя из принципа левых корней характе-стического уравнения, устанавливает следующее условие устойчивости; линейная АСР будет устойчива, если все элементы первого столбца таблицы Рауса положительны, т. е. b11>0, b21>0; br1>0.
Критерий Рауса легко реализуется с помощью современных цифровых ЭВМ с использованием типовой программы для ЭВМ. Неудобство критерия Рауса — трудность анализа влияния параметров АСР на устойчивость.
Критерий Гурвица. Для определения устойчивости АСР по критерию Гурвица характеристическое уравнение также приводится к виду ( 2 ). Далее из коэффициентов характеристического уравнения составляются определители Гурвица по форме:
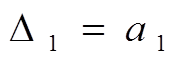 ,
,
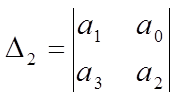 ,
,
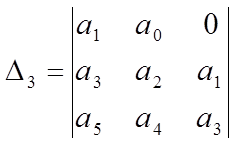 ,
,
где n — порядок уравнения АСР.
Общее правило
составления определителей Гурвица сводится к следующему: число строк и столбцов
определителя ![]() равно k;
равно k;
по диагонали определителя располагаются коэффициенты характеристического уравнения от а1_ до ak; слева от диагонали на каждой строке располагаются коэффициенты с возрастающими индексами, вправо—с убывающими, причем правее a0 пишутся нули; все коэффициенты с индексами, значения которых превышают степень характеристического уравнения, заменяются нулями. Характеристическое уравнение перед составлением определителей Гурвица должно быть приведено к такому виду, при котором a0>0.
Критерий устойчивости Гурвица сводится к следующему: линейная АСР будет устойчива, если все коэффициенты характеристического уравнения и все п определителей Гурвица положительны.
Условия устойчивости АСР невысокого порядка определяются простыми соотношениями коэффициентов характеристического уравнения, вытекающими из критериев Рауса и Гурвица. В частности, для систем 1-го и 2-го порядка признаком устойчивости является положительность всех коэффициентов характеристического
Структура определителей Гурвица показывает, что последний определитель Dn АСР равен
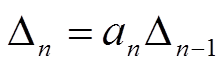 ,
,
а уравнением границы устойчивости АСР является
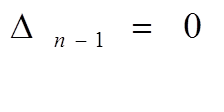
Помимо критериев Рауса и Гурвица к числу алгебраических критериев устойчивости линейных АСР относится критерий И. А. Вышнеградского, обоснование которого рассмотрено во многих специальных трудах по теории автоматического регулирования. Хотя критерий И. А. Вышнеградского разработан для анализа линейных систем 3-го порядка, заложенные в нем идеи сыграли большую роль в общем развитии теории устойчивости АСР.
Важным достоинством критерия И. А. Вышнеградского является возможность выделения в плоскости коэффициентов характеристического уравнения, а следовательно, в плоскости параметров АСР, диапазона изменения двух параметров АСР 3-го порядка, в котором система устойчива и сохраняется однотипный характер переходного процесса: монотонный, колебательный, апериодический.
В практике анализа АСР помимо алгебраических критериев широко используются частотные критерии устойчивости, основанные на анализе форм частотных характеристик, отвечающих условиям устойчивости. Для этой цели используются амплитудно-фазовые и логарифмические амплитудно-фазовые частотные характеристики, получаемые из выражений передаточных функций АСР.
Критерий устойчивости Михайлова принадлежит к числу частотных критериев и позволяет оценивать устойчивость замкнутой системы по виду годографа, который может быть получен из.характеристического уравнения.
Небходимые и достаточные условия устойчивости системы в замкнутом состоянии определяет.
формула
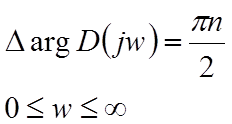
которая одновременно является математической формулировкой критерия устойчивости Михайлова.
Годограф вектора D (jw) является характеристической кривой или кривой Михайлова. Критерий устойчивости имеет следующую формулировку: для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы вектор, описывающий своим концом кривую Михайлова при изменении частоты и от 0 до + ¥, начав свое движение с положительной действительной оси и вращаясь против часовой стрелки, последовательно проходил п квадрантов, нигде не обращаясь в нуль,
Если условия, сформулированные в критерии, нарушаются, то система становится неустойчивой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.