Анализ устойчивости линейной системы автоматического регулирования: Методические указания к лабораторным работам по курсу "Теория автоматического управления"

Министерство образования Российской Федерации

Комсомольский-на-Амуре государственный технический университет

Кафедра электропривода и автоматизации

промышленных установок

АНАЛИЗ УСТОЙЧИВОСТИ ЛИНЕЙНОЙ САР

Методические указания к лабораторным работам по курсу

«Теория автоматического управления»

Комсомольск-на-Амуре 2005

УДК 62.50

          Анализ устойчивости линейной системы автоматического регулирования: Методические указания к лабораторным работам / Сост. С. В. Стельмащук. – Комсомольск-на-Амуре: Комсомольский-на-Амуре гос. тех. ун–т, 2005. – 11 с.

Данное методическое пособие предназначено для практической проработки навыков по анализу устойчивости линейной САР по расположению корней характеристического уравнения САР, а также используя критерии Гурвица, Михайлова и Найквиста. Для выполнения данной лабораторной работы необходимы знание правил структурного преобразования и умение рассчитывать графики частотных характеристик.

          Предназначено для студентов специальностей 220201 и 140604.

          Печатается по постановлению редакционно-издательского совета Комсомольского-на-Амуре государственного технического университета.

          Согласовано с отделом стандартизации.

ЦЕЛЬ РАБОТЫ

          Изучение критериев устойчивости линейных САР, исследование влияния величины коэффициента усиления разомкнутой системы на устойчивость линейной САР, а также использование программного приложения MathCad для анализа устойчивости САР.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Под устойчивостью САР понимается её способность возвращаться в установившееся состояние, из которого система была выведена после исчезновения внешнего воздействия.

Экспериментально устойчивость наглядно можно наблюдать по графику переходной функции. Если САР устойчива, то переходная функция такой системы стремится к новому установившемуся значению и переходный процесс носит апериодический или колебательный затухающий характер (рис.1). В случае неустойчивой САР переходный процесс, либо неограниченно возрастает, либо носит колебательный характер с непрерывно возрастающей амплитудой (рис.2). Переходный процесс САР, находящейся на границе устойчивости, представляет собой незатухающие колебания с постоянной амплитудой.

	Рис.1 Графики переходных процессов для устойчивой системы		Рис.2 Графики переходных процессов для неустойчивой системы

 

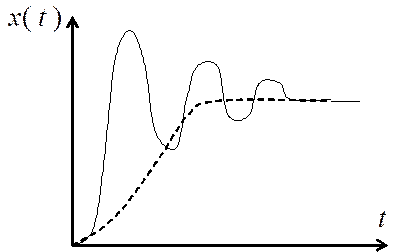
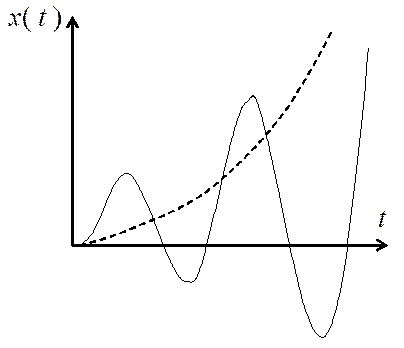
В общем случае устойчивость линейной непрерывной САР определяется корнями характеристического уравнения, которое получено равенством знаменателя передаточной функции САР нулю. Таким образом, если задана САР с передаточной функцией

,

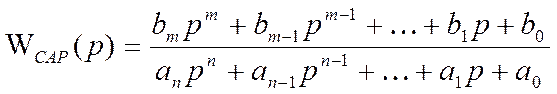то характеристическим уравнением будет являться выражение

,

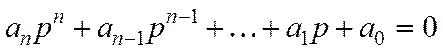а корни данного уравнения определим через переменные , которые в общем случае являются комплексно-сопряжёнными, действительными или чисто мнимыми. Для удобства анализа устойчивости корни характеристического уравнения САР располагают на комплексной плоскости.

По корням характеристического уравнения в соответствии принципом А.М. Ляпунова определяется устойчивость САР:

1.  Если все корни имеют отрицательную вещественную часть, то САР является устойчивой. Таким образом, для того чтобы САР была устойчивой, все корни должны находиться в левой полуплоскости комплексной плоскости. Эта область изображена на рис.3а заштрихованной. Корни, расположенные в левой полуплоскости называются левыми.

2.  Если хотя бы один корень имеет положительную вещественную часть, т.е. находится в правой полуплоскости (правый корень), то САР является неустойчивой. Данный случай неустойчивой САР изображён на рис.3б, где правым корнем является корень l ₃.

3. 

Если корни имеют отрицательную вещественную часть за исключением хотя бы двух чисто мнимых, которые располагаются на мнимой оси комплексной плоскости, то САР находится на границе устойчивости. Такими корнями являются l ₁ и l ₂ на рис.3в.

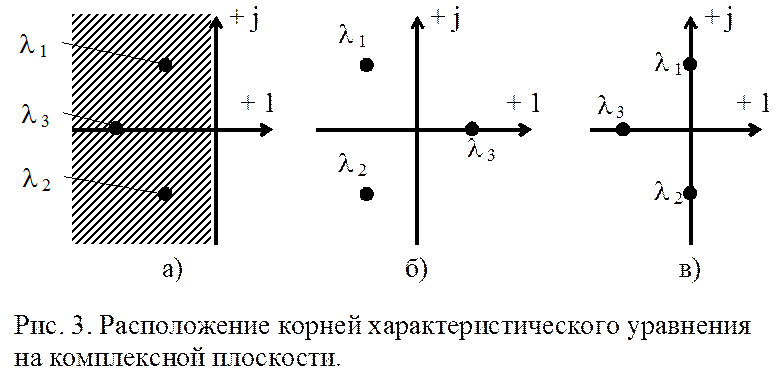При использовании MathCad для определения корней полинома применяется функция polyroots(a), где a – вектор коэффициентов полинома, который заполняется начиная со свободного коэффициента.

Критерий Гурвица

Для определения устойчивости САР по критерию Гурвица необходимо располагать характеристическим полиномом (знаменателем передаточной функции) всей системы (или замкнутой системы).