Анализ устойчивости линейной системы автоматического регулирования: Методические указания к лабораторным работам по курсу "Теория автоматического управления", страница 3

D-разбиение осуществляется используя характеристическое уравнение всей системы (или замкнутой системы). Для этого группируют члены уравнения которые зависят от исследуемого параметра, и члены – которые не зависят от исследуемого параметра.

Далее, исследуемый параметр k₁ выражается из данного равенства с левой стороны и, заменяя оператор p на jw, получается годограф исследуемого параметра k₁(jw).

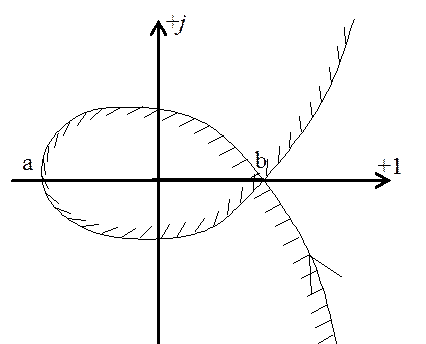
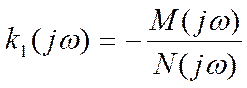
При изменении w от -¥ до +¥ график k₁(jw) будет представлять собой петлеобразную кривую, левую сторону которой, по направлению увеличения w, заштриховывают (рис.8).

В результате образуются области (D-области) ограниченные кривой годографа исследуемого параметра k₁(jw). Причём, D-область полностью ограниченная заштрихованной кривой представляет собой область значений исследуемого параметра, при которых САР будет устойчивой. Но поскольку исследуемые параметры принимают вещественные значения, а D-область это область комплексных значений, то из всей заштрихованной D-области представляет интерес отрезок (a,b) на вещественной оси. В большинстве случаев коэффициент усиления это параметр, принимающий положительные значения, следовательно, искомая область значений коэффициента k₁ при которых САР будет устойчивой это отрезок (0,b), определяющий область 0<k₁<b. Причём точка b это значение коэффициента k₁, при котором САР будет на границе устойчивости, поэтому данное значение k_1гр=b будем называть граничным.

Для определения граничного значения k_1гр необходимо вычислить значение частоты w`, при которой выполняется условие

.

При этом, граничное значение определяется из выражения

.

ПРОГРАММА РАБОТЫ

1.   Осуществить D-разбиение относительно коэффициента усиления передаточной функции W₁(p). Определить величину коэффициента k_1гр при котором система находилась бы на границе устойчивости.

2.   Получить переходные функции и определить корни характеристического уравнения замкнутой системы при а) k₁ = k_1гр; б) k₁ = 10k_1гр; в) k₁ = k_1гр/10 (корни характеристического уравнения зарисовать на комплексной плоскости).

3.   При всех трёх k₁, приведённых выше, определить устойчивость САР по критериям Гурвица, Михайлова и Найквиста.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1.   Что такое замкнутая и разомкнутая системы?

2.   Как получить характеристическое уравнение?

3.   Где должны располагаться корни характеристического уравнения на комплексной плоскости для того чтобы система была устойчивой?

4.   Чем необходимо располагать для определения устойчивости по критерию Гурвица?

5.   По чему определяется устойчивость системы в соответствии с критерием Михайлова?

6.   Основные признаки годографа Михайлова для устойчивости системы.

7.   Что представляет собой годограф Найквиста?

8.   Как определить устойчивость системы по критерию Найквиста?

ВАРИАНТЫ ЗАДАНИЙ

Задана структура

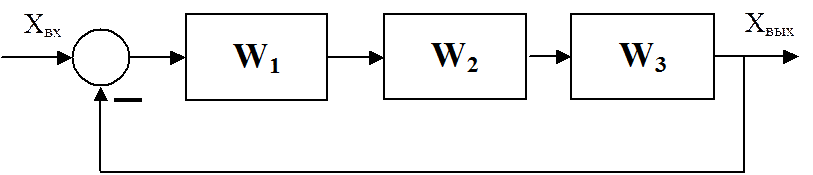
По таблице выбирается вариант

№	W1	W2	W3
1
2
3
4

Продолжение таблицы вариантов

№	W1	W2	W3
5
6
7
8
9
10
11
12
13
14
15
16
17
18

Продолжение таблицы вариантов

№	W1	W2	W3
19
20
21
22
23
24

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.   Воронов А.А. Основы теории автоматического управления.— М.; Л.: Энергия, 1965.

2.   Бесекерский В.А., Попов Е.П. Теория автоматического управления.— СПб.: Профессия, 2004.