Анализ устойчивости линейной системы автоматического регулирования: Методические указания к лабораторным работам по курсу "Теория автоматического управления", страница 2

Из коэффициентов характеристического полинома составляется матрица Гурвица размером n´n.

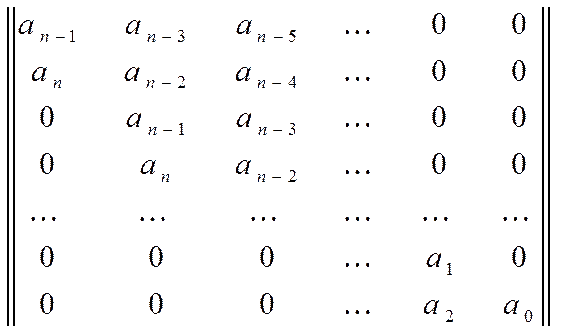
По критерию устойчивости Гурвица следует, что при a_n > 0, для того чтобы система была устойчивой необходимо, чтобы все n определителей по главной диагонали квадратной матрицы коэффициентов были больше нуля . Если хотя бы один определитель будет меньше нуля, то система будет неустойчива. Если хотя бы один определитель будет равен нулю, то система будет на границе устойчивости.

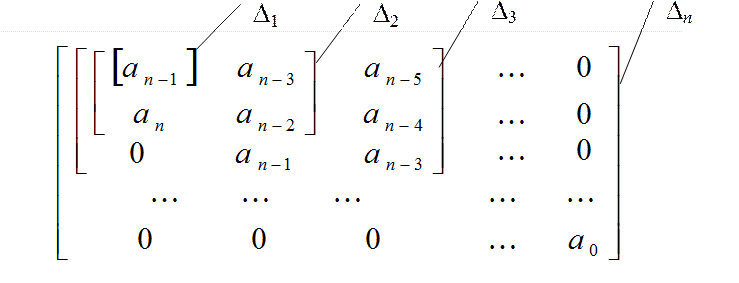
При использовании MathCad для ввода матрицы применяется комбинация клавиш Ctrl + M, а определитель матрицы есть модуль матрицы.

Критерий Михайлова

Устойчивость САР по критерию Михайлова определяется по годографу характеристического полинома всей системы (или замкнутой системы).

Если 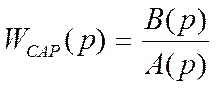, то характеристическим годографом является выражение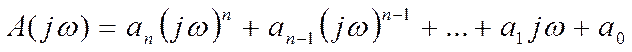

При изменении w от нуля до бесконечности график A(jw) будет представлять собой кривую называемую годографом Михайлова. Если характеристическое уравнение будет иметь l правых корней и (n– l) левых, то в результате полное приращение фазы годографа характеристического полинома при изменении w от нуля до бесконечности составит

.

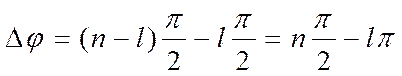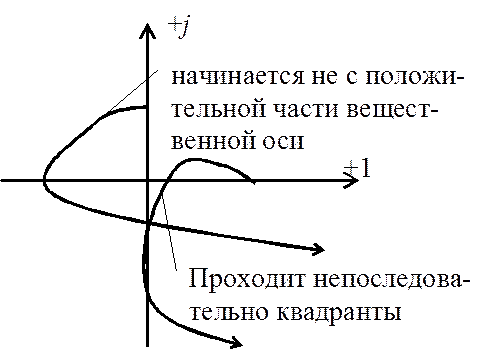
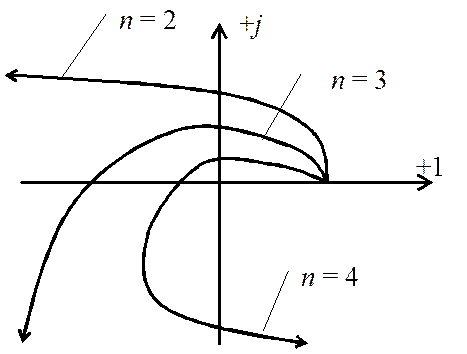Этим выражением определяется связь между формой годографа Михайлова и знаками вещественных частей корней характеристического уравнения. Годограф Михайлова для устойчивых систем имеет спиралевидную форму, причём начинается он на положительной части вещественной оси и последовательно проходит против часовой стрелки n квадрантов. Причём конец его вектора уходит в бесконечность в том квадранте комплексной плоскости, номер которого равен степени характеристического уравнения (рис.4). Неустойчивость системы связана с нарушением прохождения квадрантов (рис.5).

	Рис.4 Годографы Михайлова для устойчивой системы		Рис.5 Годографы Михайлова для неустойчивой системы

 

Критерий Найквиста

Устойчивость САР замкнутой отрицательной обратной связью по критерию Найквиста определяется по годографу передаточной функции разомкнутой САР (годографу Найквиста).

Если задана передаточная функция разомкнутой системы 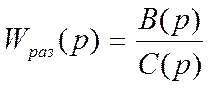, то для замкнутой системы с отрицательной обратной связью передаточная функция представляет собой

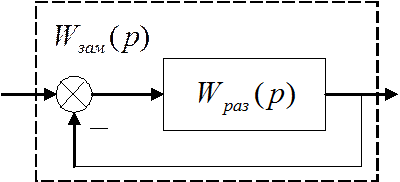
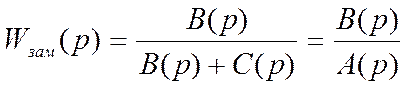
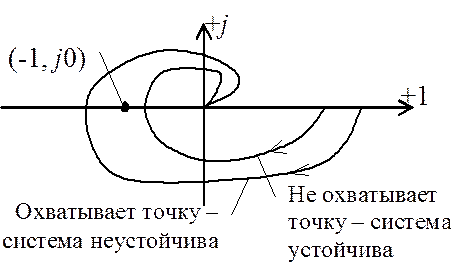
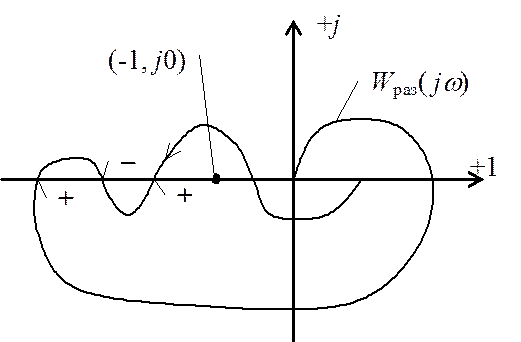
Для того чтобы система была устойчивой в замкнутом состоянии по критерию Найквиста необходимо, чтобы полное приращение фазы годографа Найквиста относительно точки на комплексной плоскости с координатами (-1; j0) при изменении частоты от нуля до бесконечности составил Dj = 2lp., где l это число правых корней характеристического уравнения разомкнутой системы C(p) = 0. Из этого следует, что для определения устойчивости системы в замкнутом состоянии необходимо знать число правых корней разомкнутой системы l, т.е. необходимо знать устойчивость разомкнутой системы.

Выражение для Dj определяет связь между формой годографа Найквиста и знаками вещественных частей корней характеристического уравнения замкнутой системы. Для того чтобы система в замкнутом состоянии была устойчивой необходимо чтобы годограф Найквиста охватывал точку (-1; j0)  раз (рис.6).

Для более сложного поведения годографа Найквиста охват точки     (-1; j0) оценивается по количеству отрицательных N_– и положительных N₊ переходов годографа Найквиста через вещественную ось левее точки с координатами (-1; j0). Причём, если переход годографом по направлению увеличения частоты производится сверху вниз, то такой переход считается положительным, а снизу вверх – отрицательным. В этом случае, устойчивость системы определяется из выражения

.

Если данное равенство выполняется, то система устойчива. В противном случае – неустойчива. Из примера на рис.7 следует, что для разомкнутой системы с двумя правыми корнями (l = 2) в замкнутом состоянии будет устойчивой т.к. N₊ = 2, N_– = 1, следовательно, выполняется равенство .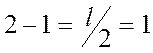

Для получения годографов в приложении Mathcad необходимо в передаточной функции заменить оператор pна произведение 1i×w. Величина 1i является мнимым числом в MathCad. Таким образом, если имеется некоторая передаточная функция W(p), то годограф данной функции представляет собой

P(w) = Re(W(1i×w)) – вещественная частотная характеристика,

Q(w) = Im(W(1i×w)) – мнимая частотная характеристика.

D-разбиение

Методика D-разбиения применяется для определения областей значений одного, двух и более исследуемых параметров САР, при которых САР будет либо устойчивой, либо неустойчивой. В данном пособии рассматривается определение области значений коэффициента усиления k₁ передаточной функции W₁(p), при которых САР будет устойчивой.