Основы теории преобразования частоты на СВЧ, страница 3

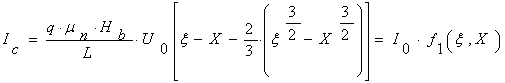
                         (2.9)                    

где

      ,    .

В   режиме   насыщения   Ic   =I.   В   случае   круглого   канала   общий   вид соотношений (2.7.,2.8.,2.9.) остается неизменным, но добавляется множитель:

         ,

       где  / -отклонение внешнего радиуса затвора к внутреннему радиусу.

При /  (что обычно имеет место на практике) этот множитель близок к единице. Таким образом, параметры ПТ не зависят от формы канала. Для расчета параметров часто применяют и "степенную форму":

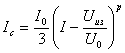                                 (2.10)

величина р зависит от профиля легирования канала и находится в пределах (1,5-2,7). Другими параметрами, определяющими частотные свойства ПТ, являются его межэлектродные емкости. Известны два метода его расчета. Один из методов сводится к интегрированию выражения для бесконечно малого участка затвора и емкости, которая берется равная емкости обратно смещенных плоских р-n переходов. С помощью другого метода можно рассчитать емкости, дифференцируя выражения для заряда обедненного слоя по электродным напряжениям:

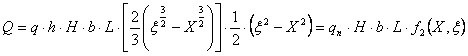  (2.11)

         В режиме насыщения Iс согласно приближению с плавным изменением канала s = I и Ссз=0. Однако, в реальных структурах  не является универсальным. Отсутствие плавности изменения канала в реальных ПТ, объясняется нарушением электронейтральности проводящей части канала, а также изменением соотношения между составляющими напряженности электрического поля, направленного вдоль направления тока и перпендикулярно ему. Результаты численных расчетов и экспериментальных исследований показали, что приближение с плавным изменением канала являются достаточно точными, если длина канала много больше толщины : L>H. Если же эти две величины соизмеримы, то плавность изменения канала нарушается. При аналитическом описании работы ПТ с коротким каналом, зависимость подвижности носителей заряда в канале от напряженности электрического поля обычно апроксимируется одним или несколькими аналитическими выражениями, например, для GaAs:

       .

При аналитических расчетах параметров ПТ обычно используют более простые аппроксимации: кусочно-линейную (рис.3.3.) и плавную. В первом случае предполагается, что при относительно малых напряженностях электрического поля подвижность носителей заряда не зависит от напряженности поля, и выполняются другие допущения Шокли. При с дифференциальная подвижность становится равной нулю. Насыщенность тока наступает тогда, когда выполняется уравнение:

              (2.12)                        

 Из уравнения (3.12.) можно найти напряжение насыщения тока стока. В пологой области ВАХ напряженность поля стока резко возрастает, и носители двигаются с постоянной скоростью. Поэтому при использовании кусочно-линейной аппроксимации канал делят на две области (рис.2.4.). В области 1, прилегающей к истоку- E>Es, а в области прилегающей к стоку- E<Es. Аналитический расчет был проведен Греблиш и Гренди . Решая двумерное уравнение Пуассона для этой области и полагая, что носители двигаются с постоянной скоростью, а толщина не отсеченной области много меньше общей толщины канала, т.е., они получили решение в виде:

              (2.13)                 

Стец, Хауз, Пуассон, воспользовавшись (2.7.,29.), рассчитали входную проводимость ПТ в режиме насыщения Iс и выходную крутизну ВАХ, получили следующие зависимости:

Кусочно-линейная апроксимация зависимости скорости дрейфа электронов от напряженности электрического поля показана на рис 2.3