
























3. ІГРИ ДВОХ ОСІБ З ДОВІЛЬНОЮ СУМОЮ
Все суєта суєт та ловля вітру.
(Соломон)
Клас неантагоністичних ігор двох осіб з довільною сумою значно ширше класу антагоністичних ігор, потребує для розв’язку конфліктних ситуацій більшого різноманіття математичних моделей, а значить, збільшує труднощі в розрахунках. Але дослідження та ідеї попередніх розділів залишаються основоположними й при розробці нових моделей гри, потребуючи лише подальшого розкриття застосувань.
3.1 Основні означення, теореми, математичні моделі
біматричної гри
Розглянемо скінчену безкоаліційну гру для двох осіб. Зазвичай в такій грі задають дві матриці однакового розміру виграшів першого і другого гравців. Строки цих матриць відповідають стратегіям першого гравця, а стовпці матриць - стратегіям другого гравця . При цьому в першій матриці представлені виграші першого гравця, а в другій матриці - виграші другого.
Означення 3.1. Гра, що задається сукупністю об’єктів ![]() де X, Y – непусті множини і функції
де X, Y – непусті множини і функції ![]() , називається біматричною
грою. Елементи
, називається біматричною
грою. Елементи ![]() називаються
стратегіями гравців 1 і 2, елементи декартового добутку
називаються
стратегіями гравців 1 і 2, елементи декартового добутку ![]() - ситуаціями, функції KХ, КY
– функціями виграшів гравців 1 та 2 відповідно.
- ситуаціями, функції KХ, КY
– функціями виграшів гравців 1 та 2 відповідно.
Відзначимо, що антагоністична гра, модель якої представлена в попередніх параграфах, є спеціальним видом біматричних ігор для якої KХ = - КY. В загальному разі біматрична гра – це гра з ненульовою сумою і кожний гравець одержує в ній свій приз (максимізує виграш). Вважаємо, що виграш є дійсним числом, яке показує ступінь досягнення бажаного результату.
Так як матриці виграшів гравців одного порядку (m×n), то біматричну гру представимо однією матрицю (таблицею), кожний елемент якої складається з двох чисел, розділених комою, перше з яких показує виграш першого гравця, друге – другого
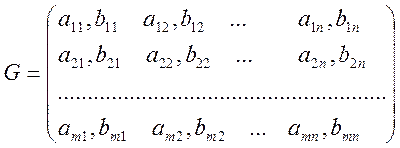 . (3.1)
. (3.1)
Наприклад, змодельована в попередньому «Дилема ув’яз-нених» (прикл.1.3) має матрицю гри
|
В1 |
В2 |
||
|
зізнатись |
не зізнатись |
||
|
А1 |
зізнатись |
5 років, 5 років |
3 місяці, 9 років |
|
А2 |
не зізнатись |
9 років, 3 місяці |
1 рік, 1 рік |
У кожного гравця цієї дилеми маємо по дві стратегії і кожна ситуація гри приписує кожному з них число, що відображає ступінь задоволення його інтересів в цій ситуації (наприклад ситуація (А1,В1) принесе результат першому гравцеві 5 років і другому гравцеві теж 5 років)). Щоправда, «виграшем» будь який результат в цій грі назвати важко.
При дослідженнях біматричних ігор постають ті ж самі питання теорії ігор: які оптимальні стратегії гравці повинні обрати в грі і які виграші при цьому вони одержать? І відразу постає ще одне питання – які розрахунки дадуть відповіді на поставленні вище питання? В пригоді знову стає поняття рівноваги.
Відповімо на поставлені питання, не вдаючись до теоретичних міркувань, наступним чином – внаслідок того, що кожен з гравців прагне одержати максимальну корисність (виграш) в грі, потрібно побудувати таке (компромісне) рішення, яке в тому чи іншому змісті задовольнить обох гравців.
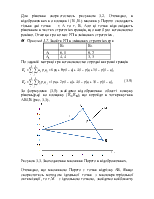
Відмінність біматричних ігор від антагоністичних полягає також в тому, що окрім рівноваги Неша (РН) та рівноваги в домінуючих стратегіях, в цих іграх можливі ще рівновага Парето (РП) та рівновага Штакельберга (РШ). Слід додати, що і рівноваг Неша в біматричній грі може бути декілька, що приводить до додаткових труднощів в виборі оптимальних рішень. І наостанок, хоча біматрична гра відноситься до класу безкоаліційних ігор, в деяких моделях виникає спокуса укладання між гравцями угод щодо вибору ситуацій в грі з додатковим розподілом між собою виграшів ( щось на зразок коаліційних угод), або узгодження між собою дій без додаткових платежів ( при декількох РН в грі). Якщо ж перемовини між гравцями неможливі або заборонені, то кожний гравець грає на свій розсуд та спираючись на інформацію, що йому відома. Іноді в такій ситуації діє принцип «невидимої руки Адама Сміта», що заспокоює суспільство в тому, що це може бути для нього і краще, ніж гравці мають право на домовленість.
Означення 3.2. Принцип «невидимої руки Адама Сміта». «Вільний ринок», незважаючи на те, що кожен з «ринкових агентів» максимізує власний прибуток, сприяє росту в цілому суспільного багатства, підвищує ефективність виробництва.
Основне призначення цього принципу – економіка, але його можна віднести з деякою долею скептизму і до теорії ігор.
3.2 Види рівноваги та алгоритми їх пошуку
Перейдемо до алгоритмів пошуку різного виду рівноваги.
Основна ідея пошуку залишається незмінною – потрібно знайти таку ситуацію гри, яку жодному гравцеві невигідно залишати. Зауваження. Принциповою відмінністю біматричних ігор є відсутність в них антагонізму, тому навіть при наявності рівноваги між гравцями існує реальна основа різного виду домовленості.
3.2.1 Рівновага Неша
Принципи пошуку РН залишаються незмінними, та й визначення РН має такий самий зміст, як представлений раніше.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.