Ігри двох осіб з довільною сумою, страница 2

Означення 3.3. Для гри G_N ={S_i, K_i, iÎN },  стратегії (s^*₁,s^*₂,…s^*_N) утворюють рівновагу Неша, якщо для кожного гравця і стратегія s^*_i є його найкращою відповіддю-реакцією на набір стратегій s^*_-i інших гравців, тобто s^*_i  розв’язує проблему

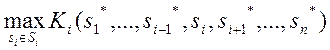    (3.2)

Теорема 3.1. Теорема Неша. В кожній скінченій біматричній грі існує рівновага в чистих або змішаних стратегіях.

Природно, що знову постає проблема доведення існування рівноваги. Рішення цієї проблеми представлено в кінці розділу в математичному відступі.

          Алгоритм пошуку РН в чистих стратегіях.

Ø   Для першого гравця обираємо його найкращі відповіді на дії другого гравця. З цією метою в кожному стовпчику (фіксуємо дію другого гравця) матриці (3.1) відмічаємо (підкреслюємо) найбільший виграш серед a_ij.

Ø  Для другого гравця проводимо аналогічні дії, але тепер фіксуємо кожен рядок та відмічаємо в ній  найбільший  виграш b_ij для другого гравця.

Ø  Якщо у вихідній матриці одержимо ситуацію, коли в будь якого її подвійного елемента (a_ij,b_ij) будуть відмічені обидва виграші,  то значить у грі відбудеться  рівновага Неша в чистих стратегіях, які представляють собою рядок для першого гравця та стовпчик – для другого, на перетині яких знаходиться відмічений подвійний елемент.

Ø  Якщо вказаної вище ситуації не відбулося, то РН в чистих стратегіях для даної гри не існує.

Зауваження. Відмітимо, що РН може бути декілька, або РН в чистих стратегіях зовсім може не існувати в грі.

? Приклад 3.1. Знайти РН в грі «Дилема ув’язнених»

(прикл. 1.3)

		В1	В2
		зізнатись	не зізнатись
А1	зізнатись	5 років, 5 років	3 місяці, 9 років
А2	не зізнатись	9 років, 3 місяці	1 рік, 1 рік

В даному прикладі максимізація виграшу означає знаходження мінімально можливого строку ув’язнення, тому в матриці по приведеному вище алгоритму підкреслені елементи найменшого значення ( кожен гравець прагне одержати мінімальний строк ув’язнення). Елемент матриці, що має подвійне підкреслення – це РН(зізнатись, зізнатись). Але при цьому кожний гравець одержить по 5 років ув’язнення, хоча в матриці(таблиці) гри є ситуація (не зізнатись, не зізнатись), що забезпечує кращий вихід для гравців ( обох ув’язнять на 1 рік). Це говорить про те, що РН – не являється панацеєю від «усіляких бід». Проте, яку стратегію обрали би ви самі в цій грі? Перемовини гравців тут неможливі, а ваш вибір «не зізнатись» ще не означає, що ваш «товариш по нещастю» обере теж «не зізнатись». Тобто над вами буде висіти загроза одержати 9 років ув’язнення.

? Приклад 3.2. Знайти РН в грі «сімейна суперечка»

(прикл. 1.4)

		В1	В2
		Ф	О
А1	Ф	3, 1	0, 0
А2	О	0, 0	1, 3

Даний приклад розкриває іншу проблему. За алгоритмом пошуку РН в чистих стратегіях, маємо дві рівноваги:

РН(Ф, Ф) з виграшами : К₁=3, К₂=1 та РН(О, О) з виграшами: К₁=1, К₂=3. Цей приклад вказує на іншу проблему біматричних ігор – вибір оптимальної стратегії при декількох РН. Будучи на місці чоловіка або жінки, яку стратегію оберете ви в цій грі, коли перемовини неможливі? Очевидним тут є пропозиція для молодят – потрібно домовлятись в такого роду іграх! Це буде корисним і гравцям і суспільству в цілому.

          ? Приклад 3.3. Знайти РН в грі, представленій матрицею(таблицею)

За алгоритмом пошуку РН одержимо РН(А₁,В₂), К₁=15,К₂=15.