Ігри двох осіб з довільною сумою, страница 3

Природно, що така рівновага гравця А не задовольнить, бо дуже привабливим для нього є а₂₁=1000. Тому гравець А всіма «правдами та не правдами» буде домагатись домовленості з гравцем В грати (А₂,В₁), щоб вкінці гри зі свого виграшу компенсувати шляхом доплати гравцеві В його згоду грати цей профіль стратегій (одержимо гру з побічними платежами).

? Приклад 3.4. Знайти РН в грі

	К	Л	М
А	2,3	-4,-1	-5,4
Б	-1,-3	0,-2	1,-4
В	3,2	-2,-1	-3,1

В цій  грі, за описаним вище алгоритмом, маємо 2 сукупності стратегій, які задають рівновагу Неша – це подвійно-відмічені стратегії (Б, Л) та (В,К). Очевидно, що ситуація (В,К) вигідніша ніж (Б, Л) для обох гравців. Та навіть в такій очевидній на перший погляд грі в плані вибору РН все ж попередня домовленість не буде зайвою.

          Зрозуміло, що якщо РН в чистих стратегіях в грі не відбувається та домовленості між гравцями не існує, гра стає нестійкою і гравцям слід аналогічно антагоністичній грі розширити пошук рішення на змішані стратегії:

S_A(p₁,p₂,…p_m), S_B (q₁,q₂,…q_n). Тоді середні виграші гравців А і В знаходимо відповідно (математичні сподівання): 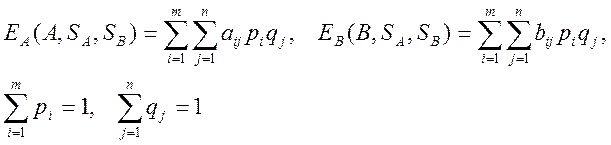(3.3)

Означення 3.4. Стратегії  S^*_A(p^*₁,p^*₂,…p^*_m),  S^*_B (q^*₁,q^*₂,…q^*_n) визначають рівноважну ситуацію, якщо одночасно виконуються нерівності

E_A(A,S^*_A,S^*_B) ≥ E_A(A,S_A,S^*_B); E_B(B,S^*_A,S^*_B) ≥ E_B(B,S^*_A,S_B)         (3.4)

          Маємо математичну модель для пошуку РН в змішаних стратегіях гри двох осіб з довільною сумою, що складається з матриці гри (3.1), співвідношень (3.3) та нерівностей (3.4). Проблема пошуку РН тісно пов’язана з аналізом найкращих відповідей R_i(s_-i) гравця і на профіль стратегій s_-i на профіль стратегій інших гравців.

          Складемо профіль найкращих відповідей всіх гравців

R(s) = (R_i(s_-i), iÎN). Зрозуміло, що s^* є РН тоді і тільки тоді, коли

s^*Î R(s^*). Таким чином існування РН тісно пов’язане з існуванням нерухомих точок відображення найкращих відповідей .

Оскільки середні виграші гравців задані функціями, що представляють полілінійні форми (3.3), то якщо зафіксувати змішані стратегії одного з гравців, середній виграш іншого стає лінійною функцією відносно його змішаних стратегій, а отже максимум цієї функції досягається в крайніх точках, тобто на чистих стратегіях. Тому, потрібно взяти всі найкращі відповіді в чистих стратегіях, та взяти всі змішані стратегії, котрі приписують ненульові ймовірності тільки оптимальним відповідям в чистих стратегіях.

          Алгоритм пошуку РН в змішаних стратегіях.

Ø Для кожного гравця виділяється деяка підмножина S⁰_i ÍS_i чистих стратегій і складається система рівнянь

E_i(s_i,m_-i) = c_i, " s_iÎ S⁰_i, iÎN. В цій системі змінними є числа c_i та ймовірності m_j(s_j) при s_jÎ S⁰_j.  Інші m_j(s_j) приймаються рівними 0, враховуючи умову 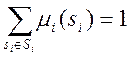. Якщо гравців тільки двоє, то система є лінійною, що обговорювалось раніше. Якщо гравців більше, то рішення такої нелінійної системи ускладнюється.

Ø Після знаходження рішення потрібно перевірити ймовірності на невід’ємність та уову найкращої відповіді

E_i(s_i,m_-i) ≤ c_i . Якщо всі умови виконані, то РН в змішаних стратегіях знайдено, якщо ні, то переходимо до іншої підмножини S⁰_i .

          Одним з відомих алгоритмів, що працює за цією схемою, є алгоритм Лемке - Хаусона, що представлений нижче. Але, якщо досліджується біматрична гра, у кожного з гравців якої маємо по дві стратегії, то пошук РН значно спрощується і навіть має зручну графічну ілюстрацію.

? Приклад 3.4. Знайти РН в змішаних стратегіях гри «сімейна суперечка», матриця якої представлена вище (прикл. 3.2).

          Ввівши змішані стратегії гравців S_A(p₁,p₂),  S_B(p₁,q₂,), за матрицею гри та співвідношеннями p₂=1- p₁ =1-р, q₂ =1- q₁=1-q складемо функції їх середніх виграшів