Ігри двох осіб з довільною сумою, страница 5

В цій грі, як неважко знайти описаним вище «методом  перебору», маємо 3 сукупності стратегій, які задають РП – це відмічені стратегії (А,К), (А,М) та (В,К). Звертаємо увагу на ту обставину, що для ситуації (А,М)  Парето-оптимальним виграшем для гравця «рядочок» є найменше значення його виграшу!

            Якщо РП в чистих стратегій в грі відсутня, то пошук РП в змішаних в біматричній грі завдає багато клопоту і вимагає пошук граничних точок спеціального характеру під назвою множина Парето (пояснення про множину Парето можна знайти в математичному відступі по цьому розділу). Знаходження РП для ігор багато в чому схоже на пошук оптимуму в багатокритеріальних задачах.

Алгоритм пошуку РП в змішаних стратегіях.

Ø Область пошуку змішаних стратегій (p,q) за відображенням К_і: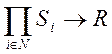переводимо на площину (К₁, К₂).

Ø Знаходимо множину Парето в відображеній області і встановлюємо рішення ( наприклад, за методом ідеальної точки), потім за цим образом знаходимо прообраз точки на множині (p,q).

? Приклад 3.6. Знайти РП в змішаних стратегіях гри «сімейна суперечка», матриця якої представлена вище (прикл. 3.2).

Для рішення скористаємось рисунком 3.2. Очевидно, в відображеннях на площині (К₁,К₂) множину Парето складають тільки дві точки – т. А та т. В. Але ці точки відповідають рішенням в чистих стратегіях гравців, що вже було встановлено раніше. Отже ця гра не має РП в змішаних стратегіях.

? Приклад 3.7. Знайти РП в змішаних стратегіях гри

По заданій матриці гри встановлюємо середні виграші гравців

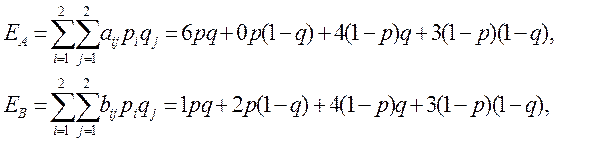(3.5)

За формулами (3.5) знайдемо відображення області пошуку рішень(p,q) на площину (Е_А,Е_В), що перейде в чотирикутник АВСВ (рис. 3.3).

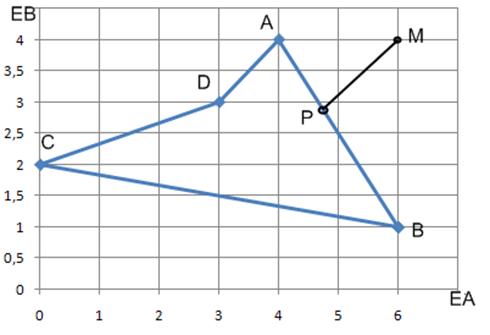
Рисунок 3.3. Знаходження множини Парето в відображеннях.

Очевидно, що множиною Парето є точки відрізку АВ. Якщо скористатись методом ідеальної точки з многокритеріальної оптимізації, то т.М – є ідеальною точкою, знайдемо найближчу точку на множині Парето, опустивши перпендикуляр з М на пряму АВ. Точка перетину цього перпендикуляру з АВ є т.P – шукана рівновага Парето. Залишилось знайти прообраз т.P на площині (p,q), щоб встановити змішані стратегії (обчисліть самостійно).

3.2.3 Рівновага Штакельберга

До цієї пори ми розглядали клас задач, коли гравці робили свої ходи одночасно. Але зачасто в економічних та менеджерських задачах, в теорії управління зустрічається математична модель, коли один із гравців «має силу влади». Тобто, саме він має владу робити перший хід. А вже всі інші гравці - будуть робити  свій хід другими. Якщо таких «інших» гравців є декілька, то вони, наприклад, можуть «розіграти» між собою рівновагу Неша. А можуть – і інший варіант концепції виграшу.

Означення 3.5. Рівновагою Штакельберга  (РШ) з лідером, який має номер 1, називається така сукупність стратегій всіх інших гравців, що перший гравець (лідер) з урахуванням цілей інших гравців прогнозує рівновагу Неша, яка буде складатися між ними після його ходу, і відповідно до цього оптимізує свою стратегію. Інші ж гравці вибирають стратегію відповідно до його прогнозу.

Зауваження. Дане означення дано за виконання наступних умов:

1. Вважається, що рівновага Неша існує для «інших» гравців для усіх можливих ходів лідера.

2. Вважається, що «інші» гравці обов’язково виберуть «у відповідь» на хід лідера саме рівновагу Неша.

Ми можемо ввести також поняття «рішення Штекельберга», розуміючи під цим, що лідер, маючи вірний прогноз щодо вибору концепції рішення «іншими» гравцями, оптимізує свій виграш з урахуванням наступних ходів інших гравців. При цьому «інші» гравці можуть розігрувати між собою, наприклад, оптимум Парето або ж свої максимінні стратегії. Таким чином, для  рішення за Штакельбергом немає необхідності, щоб «інші» гравці грали «в  рівновагу». Це означає, що поняття рішення Штакельберга має ширшу область застосування, тоді як рівновага Штакельберга виступає, найчастіше, як виняток.