Распространение радиоволн в модели радиотелефонной трассы “деревня – город”, страница 5

 

 

 

 

 

 

 

 

 

4. Оценка  изменения  поля  |E(p)|  за  препятствием

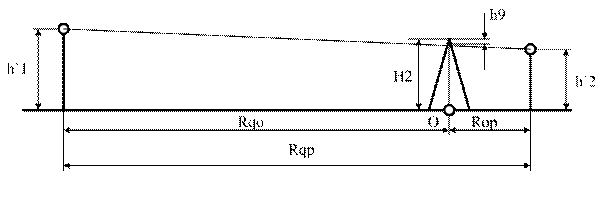
          (рис.4.1) Радиотрасса с препятствием

H₂ = 6 м   R₂ = 800м   R_op = R₂    R_qo = R_qp – R_op 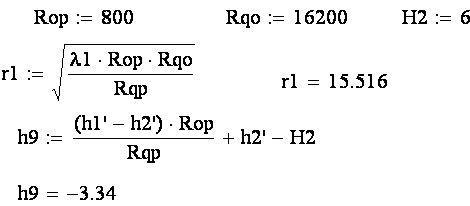           (4.1)

  Как  видно  из  расчетов  препятствие  заграждает  линию  прямого  хода  лучей  на  h9 = 3.34м,  но  вследствие  того, что  радиус  первой  зоны  Френеля  больше  высоты  препятствия  ЭМВ  будет  проходить  за  препятствие.  Так  как  угол  падения  скользящий  и  в  задании  не  оговаривается  ширина  преграды,  то  будем  считать  что  она  меньше  его  высоты H₂ = 6м. Тогда  для  оценки  поля  за  препятствием можем  воспользоваться  рис.7 и соображениями из  [4] стр. 150 – 152.

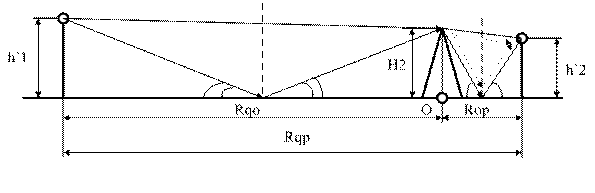
(рис.4.2) Радиотрасса с препятствием в первом приближении

Для  определения  поля  за  преградой  воспользуемся  выражением (7.45)  из  [4] стр.151. 

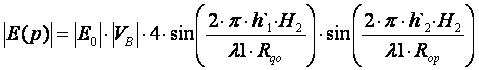        (4.2)

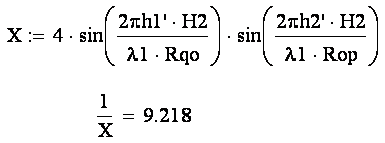                        (4.3)

Как  видно  из  расчетов  поле  за  преградой  ослабляется  в  9 раз.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5. Оценка зависимостей  |E(θ)|  и  |E(R)|  в  случае моря

     В случае прохождения радиотрассы над влажной почвой будем иметь 

ε = 30  и /Ом·м, в  результате  чего изменятся  значения W  и  k. Подставляя  новые  значения  W  и  k  в  формулы  1–го пункта,  получаем  зависимости  изображенные  на  рис.5.1 и 5.2.