Распространение радиоволн в модели радиотелефонной трассы “деревня – город”, страница 3

2. Расчет  и  построение  зависимостей  |E(θ)|  и  |E(R)|

                  

                            (рис.2.1) Радиотрасса в первом приближении

                                     Определим  модель  радиотрассы.                    

h_1изл = 3м ;         H₁ = 15 м         h₂ =  6м

    Учтем, что  передающая антенна  находится на крыше  дома  высотой H₁,  тогда общая высота подъёма передающей антенны будет равна 

h₁ = H₁ + h_1изл  = 18 м.

     Так как h₂ / λ1 = 19 > 1,  то  будем рассматривать модель радиотрассы с высоко  поднятыми антенны.

     Рассчитаем  расстояние  прямой  видимости  с  учетом  нормальной  тропосферной  рефракции.                

                                                                                       (2.1) 

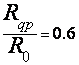                  II – модель

Т.к.  имеем  II – ю  модель  радиотрассы,  то  необходимо  учитывать  сферичность  земли, т.е.  рассчитать  приведённые  высоты  антенн.

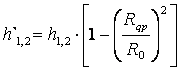                                                                                    (2.2)

                                                                                       

     Определим применимость формулы Введенского. Она является частным случаем интерференционной формулы при скользящих углах ,

Тогда полагают не только [Ф_в,г = π  ], но и |R_в,г =1 |.  Следовательно:

                      (2.3)

     При скользящих углах    и с учетом sin(x) = x (при малых углах), , получаем формулу Введенского

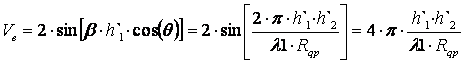
Условиями ее применимости являются условия применимости интерференционной формулы и условия малости аргумента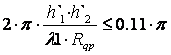                    

         При этом должны выполняться условия для земных покровов [Ф_в,г = π ] и |R_в,г =1 |. Таким образом, по формуле Введенского правильные результаты получаются только для множителя   

      Проверим условия для нашей радиотрассы:

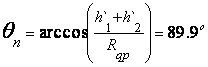
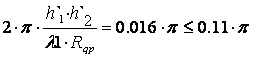                                                                        (2.4)

  Запишем  зависимость  поля  |E(θ)|  в  точке  p 

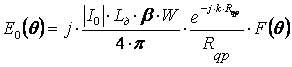                                                                (2.5)

                                                                                      (2.6)