Чисельне розв’язування нелінійного рівняння 2ex-5x-2=0 з точністю 0.0001 (Лабораторна робота № 1)

Лабораторнаробота №1

З теми „Чисельне розв’язування нелінійних рівнянь”

Вар. 9

Студент групи ІН-61

ПРОСКОЧИЛО Владислав

1.  Умова задачі

 Розв’язати нелінійне рівняння з точністю :

1 Виділити корені графічно і аналітично.

2 Розв’язати за допомогою методу простої ітерації або методу Ньютона.

2e^x-5x-2=0

2.  Математичний алгоритм

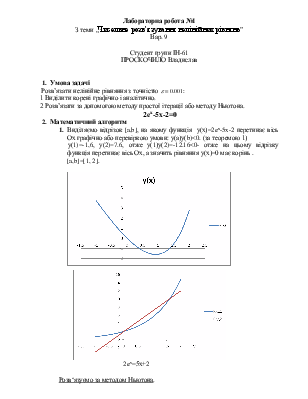
1.  Виділяємо відрізок [a,b], на якому функція  у(х)=2e^x-5x-2 перетинає вісь Ох графічно або перевіркою умови: у(а)у(b)<0. (за теоремою 1)

у(1)=-1,6, у(2)=7.6, отже у(1)у(2)=-12.16<0- отже на цьому відрізку     функція перетинає вісь Ох, а значить рівняння у(х)=0 має корінь .

[a,b]=[1, 2].

         

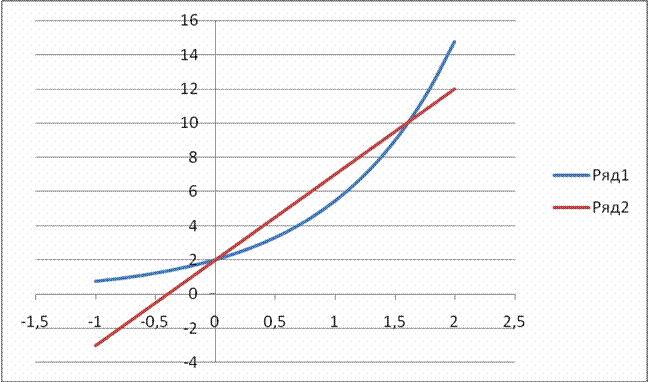
                                       2e^х=5х+2

Розв‘язуємо за методом Ньютона.

Результати

Для  рівняння 2e^x-5x-2=0 корінь, знайдений з точністю 0,001 за методом Ньютона дорівнює 1,619.

 Якщо ж узяти за точність знаходження кореня ε=10^-10 , то значення знайденого кореня рівняння буде х=1,619, що співпадає зі знайденим коренем у математичному пакеті Maple.

Якщо роздрукувати всі послідовні до заданої точності, то отримаємо:

х=1,715885;

х=1,627081;

х=1,618856;

х=1,618788;

х=1,619;