Стандартний генетичний алгоритм. Кодування і декодування параметрів

СТАНДАРТНИЙ ГЕНЕТИЧНИЙ АЛГОРИТМ (ГА)

Стандартний ГА – це метод стохастичної оптимізації для задач дискретної оптимізації вигляду «максимізувати f(s) за умови, що ». Функція називається функцією придатності;  - n-мірний двійковий вектор з дискретної множини  - хромосомою чи двійковою ниткою довжини n. Множина  є множиною вершин n-мірного гіперкуба з ребром, рівним 1; R- множина дійсних чисел.

Під двійковим вектором–хромосомою s мається на увазі двійкове подання (кодування) початкового змінного параметра V, фізичний зміст якого визначається особливостями конкретної розв’язуваної задачі. Число бітів при такім кодуванні, або довжина хромосоми n, залежить від необхідної точності визначення оптимальної величини параметра від необхідної точності визначення оптимальної величини параметра V і повинне задовольняти умову

,

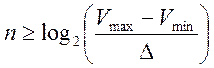де  і  - максимальне і мінімальне значення параметра V;  - задана погрішність визначення оптимального значення V.

Схема функціонування Стандартного ГА:

1. Ініціювати початковий момент часу t=0. Випадковим чином сформувати початкову популяцію, що складається з М істот. .
2. Обчислити пристосованість кожної істоти  і популяції в цілому .
3. Вибрати істоту s_c з популяції. .
4. З певною ймовірністю  вибрати другу істоту з популяції  і виконати операцію кросинговеру .
5. З певною ймовірністю  виконати операцію мутації .
6. З певною ймовірністю  виконати операцію інверсії .
7. Помістити нову хромосому в нову популяцію .
8. Виконати операції, починаючи з пункту 3, M разів.
9. Збільшити номер поточної епохи t=t+1.
10. Якщо виконалася умова закінчення роботи, то завершити її, в протилежному випадку перейти на 2.

Число істот М в популяції впливає на широту фронту пошуку.

Замість функції придатності f(s) на практиці часто розглядають її нормоване подання , отримане з вихідної функції f(s) шляхом лінійного перетворення (масштабування)

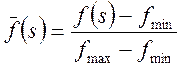
де  і  - максимальне і мінімальне значення функції .

Для пунктів 3-4 застосовуються такі схеми добору:

a)  пропорційний добір (fitness proportionate selection, FPS)

,

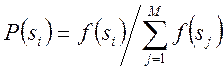b)  лінійне ранжирування (linear ranking)

де ,

c)  рівномірне ранжирування (uniform ranking)

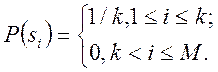
Крім того використовують процедуру елітного добору, що завжди зберігає найкращу хромосому популяції, тобто істота з найбільшою пристосованістю без схрещування переходять в нову популяцію. Використання даної процедури дозволяє прискорити збіжність ГА, але підвищує ймовірність влучення в локальний мінімум.

Кросинговер діє в такий спосіб:

-  з популяції вибираються дві істоти-предки;

-  визначається випадковим чином точка розриву хромосом;

-  хромосоми істот-нащадків визначаються як конкатенація частин хромосом першої та другої істоти-предка, потім випадковим чином вибирається одна з результуючих хромосом нащадків.

Як правило, на практиці кросинговер проводять з ймовірністю =0,6. Кросинговер може бути одноточковий та багатоточковий, коли точок розриву декілька. Граничним випадком є рівномірний кросинговер, коли відповідно до визначеної ймовірності обмінюється кожна пара генів з двох хромосом.

Кросинговер контролює баланс між використанням знайдених оптимальних областей простору пошуку і дослідженням нових. Спільне використання операторів кросинговеру та добору призводить до того, що області простору пошуку, які мають кращу в середньому оптимальність, містять більше істот, ніж інші.

Оператор мутації призначений для того, щоб підтримувати розмаїтість істот у популяції. Мутація в декількох генах хромосоми збільшує швидкість пошуку хромосомі предків на випадкові значення. Для вибору позицій таких генів і частоти мутацій використовуються ті або інші правила, наприклад, кожний черговий ген замінюється із заданою імовірністю . Мутація в декількох генах хромосоми збільшує швидкість пошуку екстремуму за рахунок більшого розкиду хромосом у просторі пошуку. Оператор мутації виконує випадкову зміну значення кожного гену з імовірністю , тобто для кожного гена хромосоми його значення змінюється з 0 на 1 чи 1 на 0 з імовірністю. Як правило, 0,001

Використовується також оператор інверсії – різновид мутації, який діє так, що хромосома поділяється на дві частини і частина хромосоми після оберту на 180º знову займає попереднє положення. Операція інверсії може бути проведена для довільного числа генів хромосоми. Після інверсії хромосоми-кандидати копіюються в нову популяцію хромосом .

Важливий момент – визначення критеріїв завершення задачі. Вони застосовуються як обмеження на максимальну кількість епох функціонування алгоритму чи визначення його збіжності, як правило, порівнянням пристосованості популяції на декількох епохах і зупинки при стабілізації цього параметра. Коли пристосованість істот перестає помітно збільшуватися, процес зупиняють і, як розв’язання задачі оптимізації, беруть найкращого зі знайдених істот.

КОДУВАННЯ І ДЕКОДУВАННЯ ПАРАМЕТРІВ

Відповідність кодів
Дес.	Двійкові	Грея
0	0000	0000
1	0001	0001
2	0010	0011
3	0011	0010
4	0100	0110
5	0101	0111
6	0110	0101
7	0111	0100
8	1000	1100
9	1001	1101
10	1010	1111
11	1011	1110
12	1100	1010
13	1101	1011
14	1110	1001
15	1111	1000

Розрізняють кодування змінних параметрів, поданих цілими числами та числами з крапкою, що плаває.

Для кодування змінних, поданих цілими числами іноді використовують війкове подання змінної, при чому довжина хромосоми повинна бути достатньою для подання всіх можливих значень даної змінної. Але основним недоліком такого способу є те, що сусідні числа відрізняються в значеннях декількох бітів. (7(0111) і 8(1000)), що ускладнює функціонування ГА і збільшує час його збіжності. Щоб уникнути цього використовують код Грея. Його можна подати як двійковий з вагами розрядів g_i=2ⁱ-1, тобто ... 15, 7, 3, 1.

При кодуванні декількох змінних необхідно провести кодування кожної у двійковий код, об’єднати отримані значення в один вектор і, розбиваючи його на тетради, перетворити за кодом Грея.

При кодуванні змінних, що подані числами з крапкою, що плаває застосовують таку послідовність:

-  поділити весь інтервал припустимих значень змінної на ділянки з необхідною точністю;

-  значення змінної визначають як номер інтервалу (ціле число), в середині якого знаходиться число.

Для коду Грея декодувальна функція має вигляд:

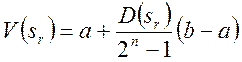
де a i b – межі відрізка [a,b], що містять значення змінної V,  - десяткове подання коду Грея.

При кодуванні нечислових даних необхідно попередньо перетворити їх у числа.