




Міністерство освіти і науки України
Сумський державний університет
Кафедра інформатики
Лабораторна робота №8
з дисципліни
«Чисельні методи»
на тему:
«Розв’язок крайової задачі Коші для ЗДР вищих порядків»
Варіант 3
Підготувала
студентка ПМ-71
Білоус Т.В.
Перевірила
Назаренко Л.Д.
Суми 2009
Розв’язати крайову
задачу для звичайного диференціального рівняння з точністю ![]()
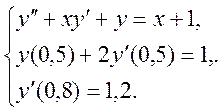
Маємо відрізок [a,b]. Потрібно знайти розв’язок лінійного диференціального рівняння другого порядку
![]() ,
(8.12)
,
(8.12)
що задовольняє такі крайові умови:
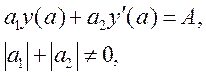
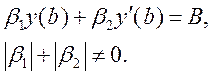 (8.13)
(8.13)
Виберемо рівномірну сітку: x = a + ih, i =
0,1,2,…,n... Нехай![]() Апроксимуємо
Апроксимуємо ![]() і
і ![]() у
кожному внутрішньому вузлі (i = 1, 2, …, n-1) центральними різницями
у
кожному внутрішньому вузлі (i = 1, 2, …, n-1) центральними різницями 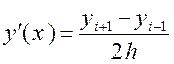 ,
, 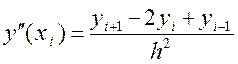 і на
кінцях відрізка – односторонніми скінченнорізницевими апроксимаціями
і на
кінцях відрізка – односторонніми скінченнорізницевими апроксимаціями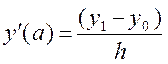 ,
, 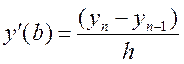 .
.
Використовуючи ці формули, одержуємо різницеву апроксимацію вихідного крайового завдання:
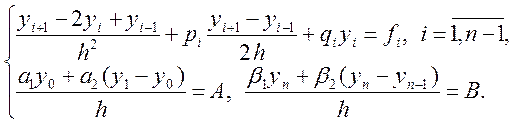 (8.14)
(8.14)
Коефіцієнти різницевих рівнянь залежать від кроку сітки.
Введемо позначення і перепишемо нашу систему:
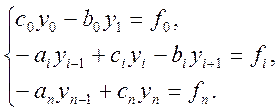
![]() (8.15)
(8.15)
Таким чином, завдання зводиться до розв’язання системи лінійних алгебраїчних рівнянь, що можна записати у вигляді Ay=F.
Отримана СЛАР розв’язувалась методом прогонки.
В першому циклі знаходились відповідні коефіцієнти 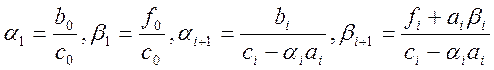 .
Значення
.
Значення ![]() знаходилось рівним
знаходилось рівним ![]() ,
а всі інші значення у - за формулою
,
а всі інші значення у - за формулою ![]() .
.
Наведемо приклад програмної реалізації знаходження розв’язку крайової задачі Коші для ЗДР вищих порядків, виконаний засобами мови програмування Сі.
Текст програми:
#include <stdio.h>
#include <conio.h>
#include <stdlib.h>
float ai(float x0,int index,float h,int n);
float bi(float x0,int index,float h,int n);
float ci(float x0,int index,float h,int n);
float fi(float x0,int index,float h,int n);
float alfa(float *al,float x0,int index,float h,int n);
float beta(float *al,float *bet,float x0,int index,float h,int n);
void main()
{
int n,i;
float a=0.5,b=0.8,h;
float *y,*aalfa,*bbeta;
clrscr();
printf("\n a=%4.1f\n",a);
printf(" b=%4.1f\n",b);
printf("\n Vvedite zhelaemoe kol-vo to4ek: ");
scanf("%d",&n);
n--;
h=(b-a)/n;
printf("\n h=%4.3f\n",h);
aalfa=(float*)malloc(sizeof(float)*(n+1));
bbeta=(float*)malloc(sizeof(float)*(n+1));
y=(float*)malloc(sizeof(float)*(n+1));
for(i=1;i<=n;i++)
{
*(aalfa+i)=alfa(aalfa,a,i,h,n);
*(bbeta+i)=beta(aalfa,bbeta,a,i,h,n);
}
for(i=n;i>=0;i--)
{
if (i==n)
{
*(y+i)=beta(aalfa,bbeta,a,n+1,h,n);
}
else
*(y+i)=alfa(aalfa,a,i+1,h,n)*(*(y+i+1))+beta(aalfa,bbeta,a,i+1,h,n);
}
printf("\n REZULTAT:\n\n");
for(i=0;i<=n;i++)
printf(" x%d=%5.3f y%d=%5.3f\n",i,(a+h*i),i,*(y+i));
printf("\n");
getch();
}
float ai(float x0,int index,float h,int n)
{
if (index>0 && index<n)
return h*(x0+index*h)-2;
if (index==n) return 0;
else
{
printf("Error!!!(ai)\n");
return 0;
}
}
float bi(float x0,int index,float h,int n)
{
if (index>0 && index<n)
return -2-h*(x0+index*h);
if (index==0) return 2;
else
{
printf("Error!!!(bi)\n");
return 0;
}
}
float ci(float x0,int index,float h,int n)
{
if (index>0 && index<n)
return 2*h*h-4;
if (index==n) return 1;
if (index==0) return h-2;
else
{
printf("Error!!!(ci)\n");
return 0;
}
}
float fi(float x0,int index,float h,int n)
{
if (index>0 && index<n)
return 2*h*((x0+index*h)+1);
if (index==n) return 1.2;
if (index==0) return h;
else
{
printf("Error!!!(fi)\n");
return 0;
}
}
float alfa(float *al,float x0,int index,float h,int n)
{
float alf;
if (index==1) alf=bi(x0,0,h,n)/ci(x0,0,h,n);
if (index>1 && index<=n)
alf=bi(x0,index-1,h,n)/(ci(x0,index-1,h,n)-(*(al+index-1))*ai(x0,index-1,h,n));
if (index>n||index<1)
{
printf("ERROR!!!(alfa)\n");
alf=0;
}
return alf;
}
float beta(float *al,float *bet,float x0,int index,float h,int n)
{
float bb;
if (index==1) bb=fi(x0,0,h,n)/ci(x0,0,h,n);
if (index>1 && index<=n+1)
bb=(fi(x0,index-1,h,n)+ai(x0,index-1,h,n)*(*(bet+index-1)))/(ci(x0,index-1,h,n)-*(al+index-1)*ai(x0,index-1,h,n));
if (index>n+1||index<1)
{
printf("ERROR!!!(beta) %d\n",index);
bb=0;
}
return bb;
}
Результат роботи програми:
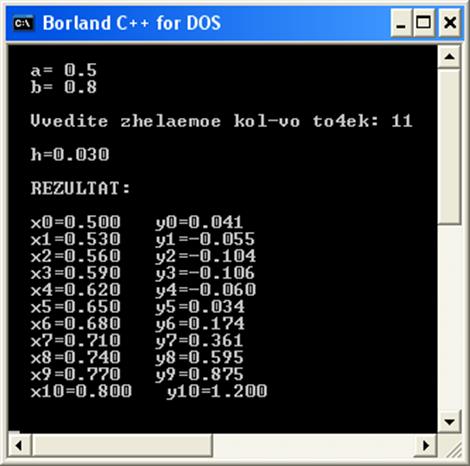
Під час пакетної реалізації було побудовано таблицю значень функції у заданих вузлах за допомогою звичайних функцій Maple.
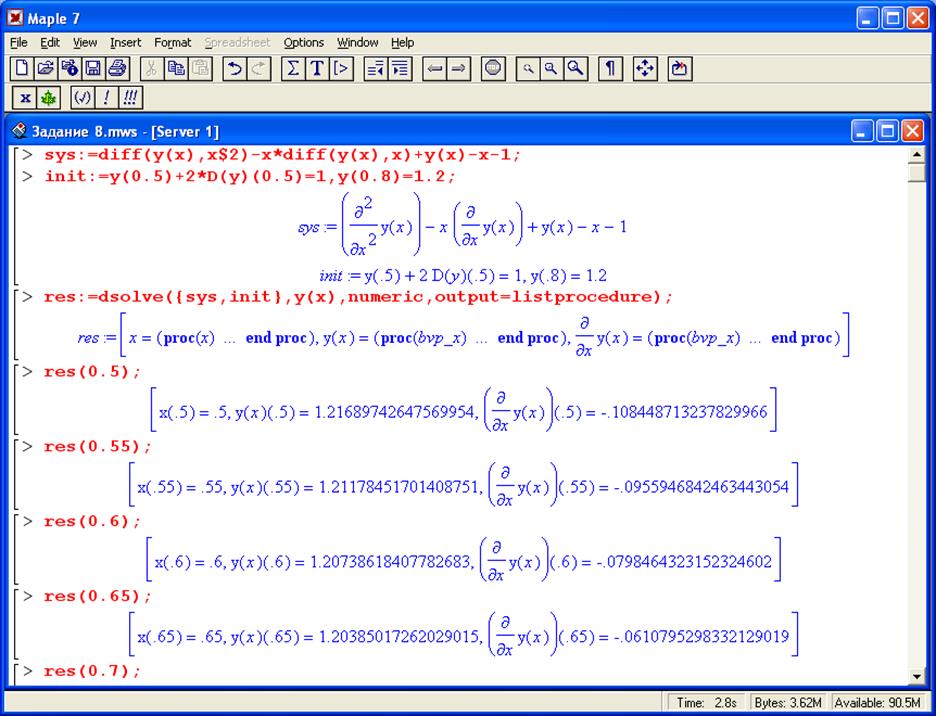
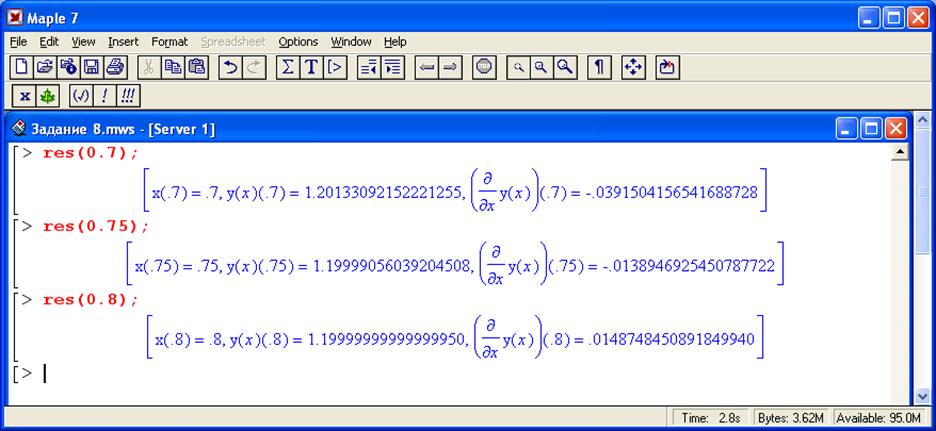
У даній лабораторній роботі було чисельно розв’язано крайову задачу Коші для диференціального рівняння другого порядку.
Дане завдання було виконане програмно та пакетно. Обидва способи реалізації даного методу досить легкі, проте результати, отримані програмно та пакетно, не збігаються, адже задача є нестійкою. Було побудовано таблицю значень функції у певних вузлах сітки, що і є чисельним розв’язком задачі.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.