









Варіант 7
ЗАДАЧА 1
Отримана
вибірка об’єму ![]() :
:
7, 1, 4+m, 3, 2+k, 16+2![]() , 15+n, 4, 1, 1,
3+k, 5,
, 15+n, 4, 1, 1,
3+k, 5,
5, 6, 6, 6, 1, 5+m, 3+n, 14+2m, 2, 2, 7, 7, 7, 4, 4,
3, 1, 2+p, 6, 8, 4, 15+3p, 1+k, 1+m, 1+n, 5, 5, 3.
В задачі потрібно:
1. Побудувати: інтервальний варіаційний ряд розподілу; гістограму; емпіричну функцію розподілу.
2. Знайти: вибіркове середнє, вибіркову дисперсію, середнє квадратичне відхилення, медіану і моду вибірки.
3. Оформити результати графічно.
Номер варіанта Параметри
7 k = 1, m = 1, n = 2, p = 0.
Запишемо задану вибірку:
7, 1, 5, 3, 3, 16, 17, 4, 1, 1, 4, 5,
5, 6, 6, 6, 1, 6, 5, 17, 2, 2, 7, 7, 7, 4, 4,
3, 1, 2, 6, 8, 4, 15, 2, 2, 3, 5, 5, 3.
Упорядкуємо задану вивірку:
1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3,
4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6
7, 7, 7, 7, 8, 15, 16, 17, 17.
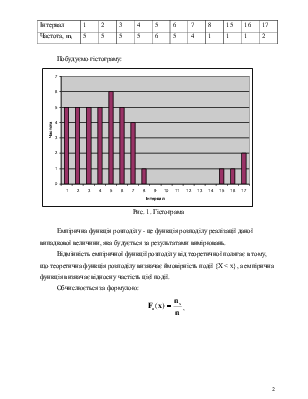
Залежність перерахованих характеристик від інтервалів ознаки називається інтервальним рядом розподілу, а її графічна інтерпретація – гістограмою розподілу.
Як характеристики розподілу об'єктів за інтервалами ознаки можуть застосовуватися частоти mi; (в одиницях або штуках), частості рi* (в кількості об'єктів, що доводяться на одиницю зміни ознаки).
Побудуємо інтервальний ряд розподілу:
|
Інтервал |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
15 |
16 |
17 |
|
Частота, mi |
5 |
5 |
5 |
5 |
6 |
5 |
4 |
1 |
1 |
1 |
2 |
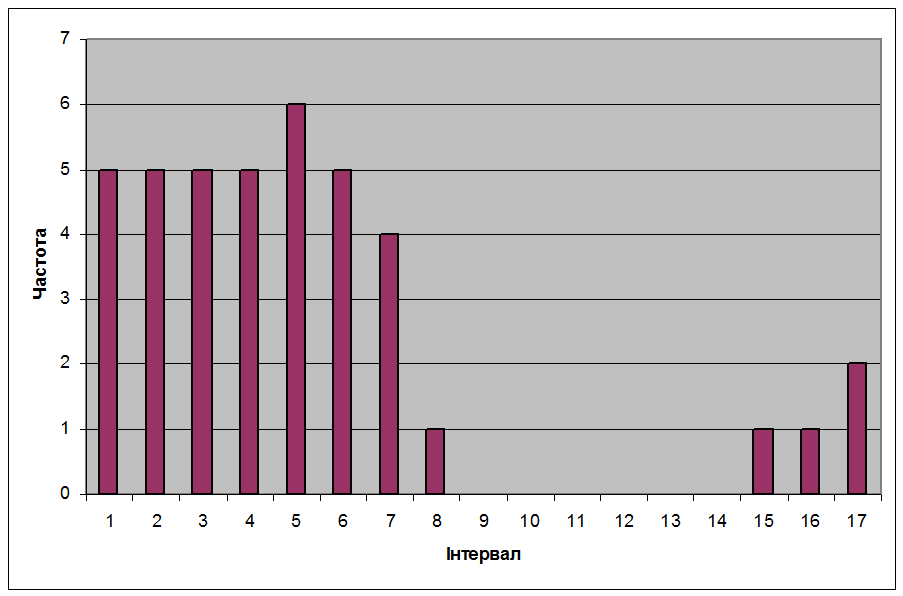 |
Рис. 1. Гістограма
Емпірична функція розподілу - це функція розподілу реалізації даної випадкової величини, яка будується за результатами вимірювань.
Відмінність емпіричної функції розподілу від теоретичної полягає в тому, що теоретична функція розподілу визначає ймовірність події {X < х}, а емпірична функція визначає відносну частість цієї події.
Обчислюється за формулою:
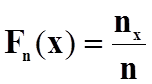 ,
,
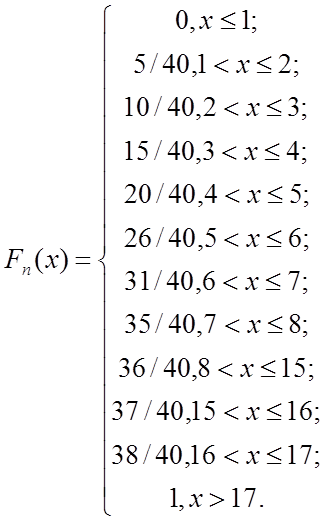 .
.
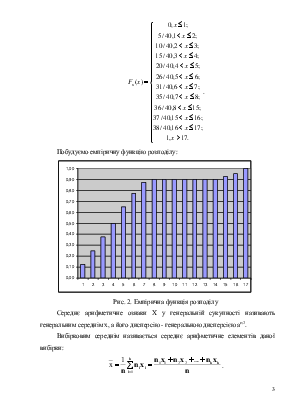
Побудуємо емпіричну функцію розподілу:
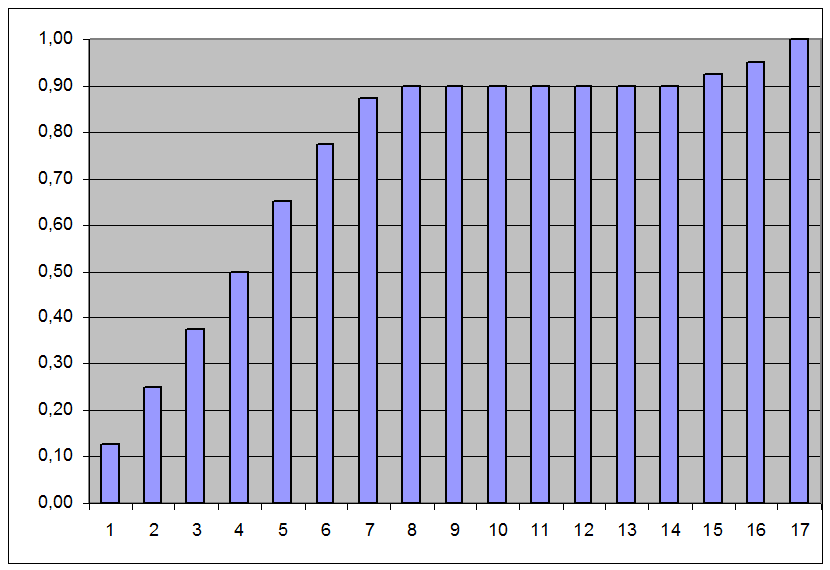
Рис. 2. Емпірична функція розподілу
Середнє арифметичне ознаки X у генеральній сукупності називають генеральним середнім х, а його дисперсію - генеральною дисперсією а"2.
Вибірковим середнім називається середнє арифметичне елементів даної вибірки:
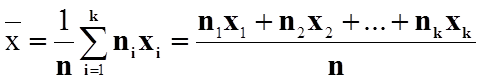 .
.
Підставимо наші значення у формулу:
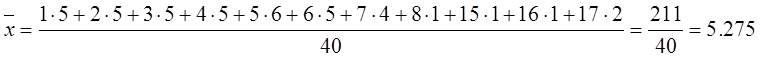
Вибіркову дисперсію обчислюємо за формулою:
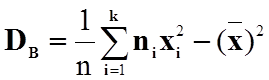 .
.
Обрахуємо вибіркову дисперсію для наших значень:
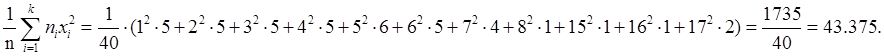
![]()
Середнє квадратичне відхилення, позначається як S або σ. — у теорії ймовірності і статистиці найбільш поширений показник розсіювання значень випадкової величини відносно її математичного сподівання.
Вибіркове середнє квадратичне відхилення обчислюємо за формулою:
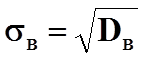 ,
,
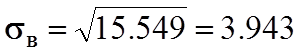 .
.
Медіану обчислюють за формулами:
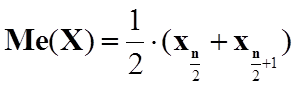 ,
,
якщо число – n парне;
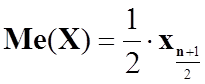 ,
,
якщо число n – непарне.
Тут беремо індекси в xi згідно з нумерацією варіант у варіаційному ряді.
У нашому випадку n=40, тому
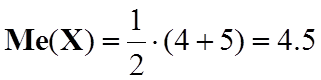 .
.
Мода – це варіанта, яка у варіаційному ряді трапляється найчастіше, тобто
![]() .
.
ЗАДАЧА 2
Випадкова величина Х задана густиною розподілу ймовірностей:
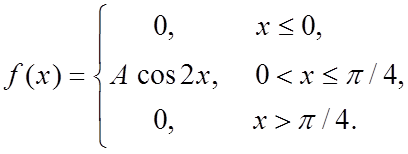
Знайти: параметр A;функцію розподілу F(x); математичне сподівання M[X]; дисперсію D[X]; ймовірність P(π/4≤X≤π). Роботу оформити графічно.
Густина f(x) будь-якої випадкової величини невід'ємна, f(x) > 0, та має властивість
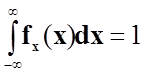 ,
,
тобто ймовірність повної групи подій дорівнює одиниці.
Коефіцієнт А визначимо за допомогою формули про ймовірність повної групи подій
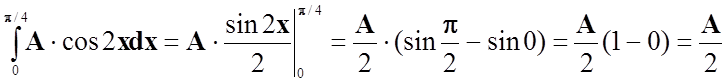 ,
,
А=2.
Тоді випадкова величина Х задана густиною розподілу ймовірностей;
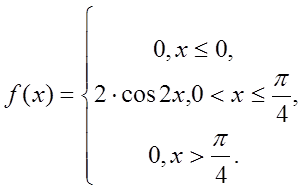
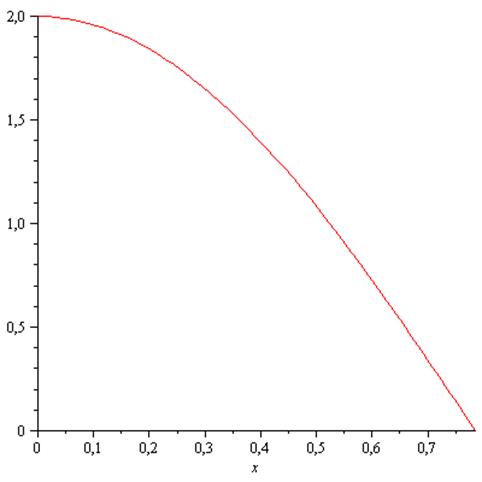
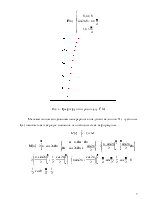
Рис. 3. Графік густини розподілу ![]()
Функція розподілу неперервної випадкової величини X виражається через її густину:
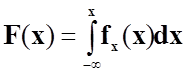 .
.
У випадку, коли x≤0,
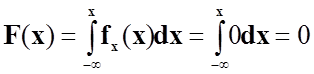 .
.
У випадку, коли 0<x≤π/4,
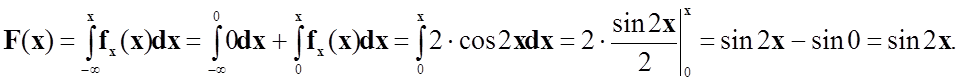 У випадку, коли
x<π/4,
У випадку, коли
x<π/4,
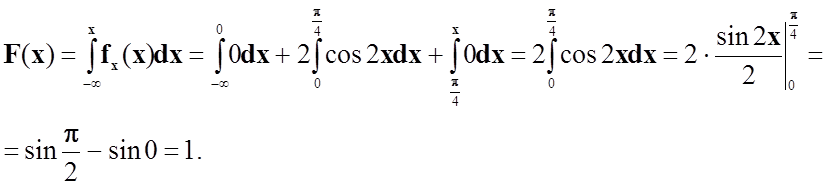
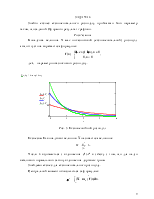
Тоді функція розподілу буде мати вигляд:
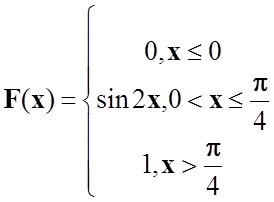 .
.
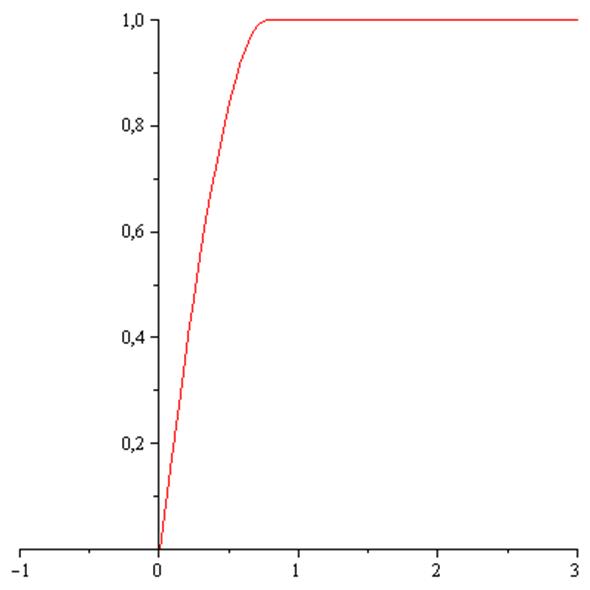
Рис. 4. Графік функції розподілу ![]()
Математичним сподіванням неперервної випадкової величини X з густиною f(x) називається її середнє значення, що обчислюється за формулою
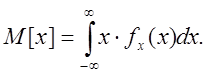
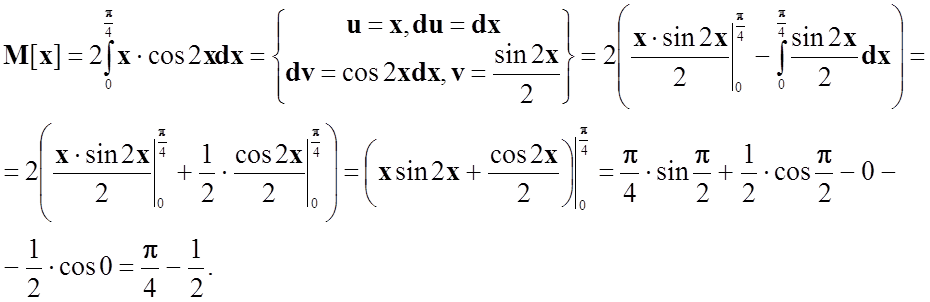
Дисперсія дорівнює математичному сподіванню квадрата випадкової величини мінус квадрат її математичного сподівання, і обчислюється за формулою:
![]() .
.
Обчислимо спочатку M[X2] - другий початковий момент:
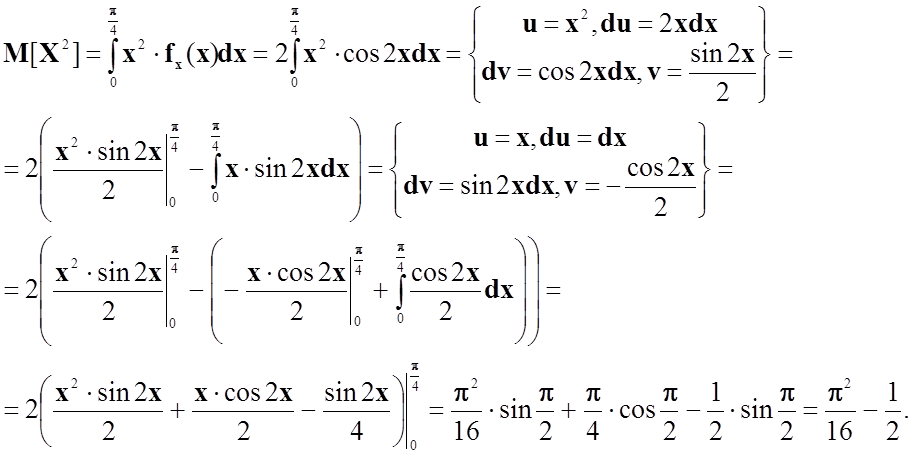
Тепер обрахуємо дисперсію:
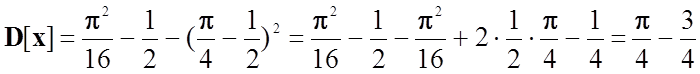 .
.
Знайдемо ймовірність P(π/4≤X≤π).
Якщо ймовірність влучення неперервної випадкової величини Х на ділянку від α до β визначається за формулою:
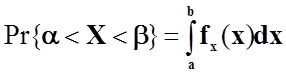 .
.
Для будь-якої випадкової величини імовірність влучення випадкової величини на ділянку від α до β визначається за формулою:
![]() ,
,
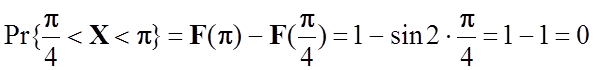 .
.
ЗАДАЧА 3
Знайти ексцес експоненціального розподілу, прийнявши його параметр таким, що заданий. Оформити результат графічно.
Випадкова величина X має показниковий (експоненціальний) розподіл, якщо її густина виражається формулою:
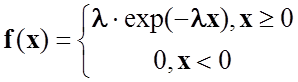 ,
,
де λ – параметр показникового розподілу.
|
|
|
|
|
Рис. 5 Експоненційний розподіл |
Ексцесом Ех випадкової величини X називається величина:
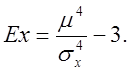
Число 3 віднімається з відношення μ4/σх4 в зв'язку з тим, що для надто важливого нормального закону відношення дорівнює трьом
Знайдемо ексцес для експоненціального розподілу.
Центральний момент обчислюється за формулою:
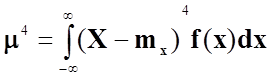 .
.
Середнє квадратичне відхилення випадкової величини обчислюється за формулою:
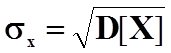 .
.
Дисперсія обчислюється за формулою:
![]()
Математичне сподівання обчислюється за формулою:
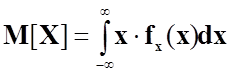 .
.
Обчислимо ексцес за заданою формулою.
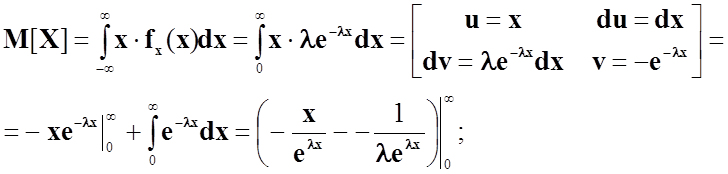
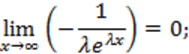
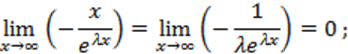
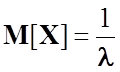 .
.
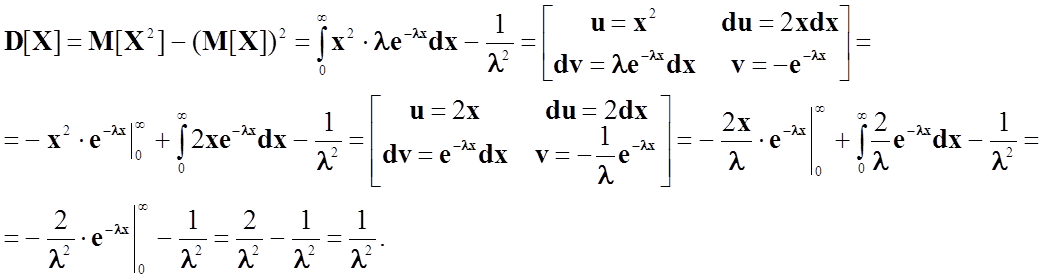
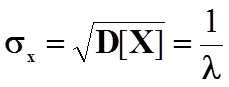 .
.
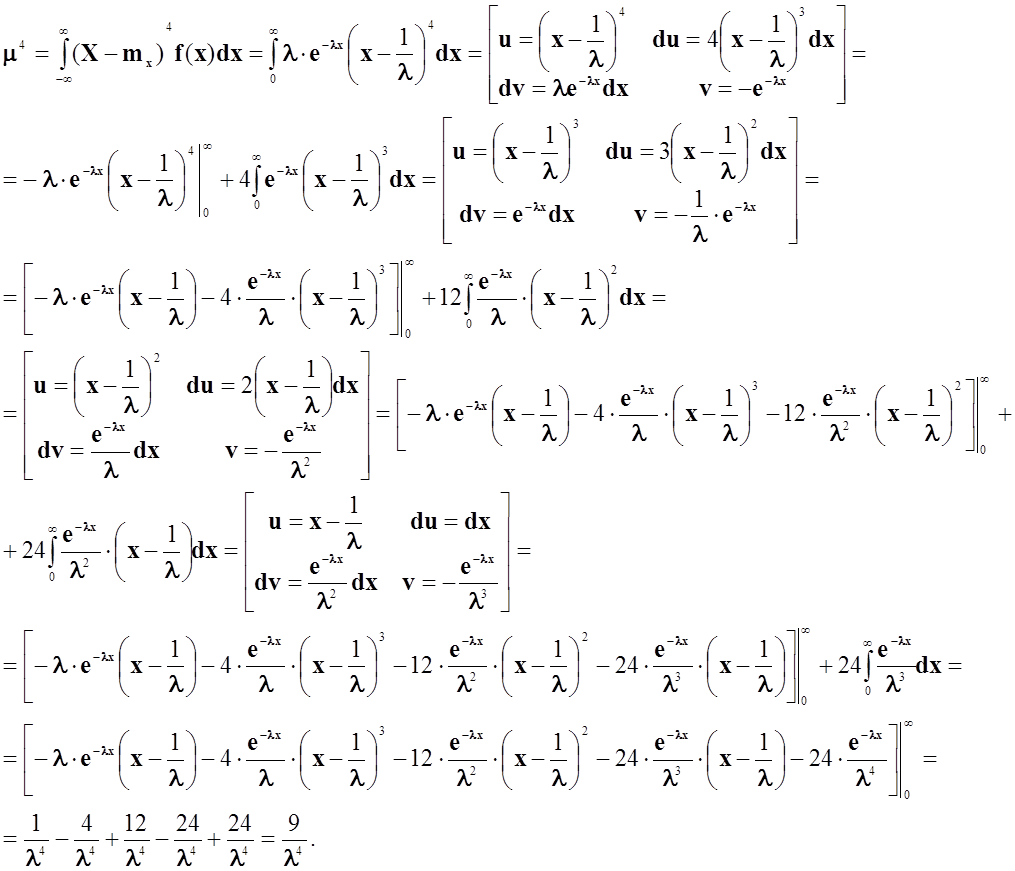
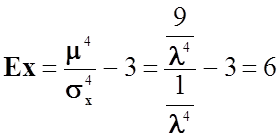 .
.
Відповідь: ексцес експоненціального розподілу дорівнює 6.
Випадкова
величина Z нормальна з нульовим математичним очікуванням і заданої дисперсії ![]() .
.
Знайти значення
дисперсії, за якою ймовірність Pr{p![]() Z
Z![]() q} буде найбільшою (параметри p
і q задані та позитивні, p
q} буде найбільшою (параметри p
і q задані та позитивні, p![]() q).
q).
Випадкова величина X має нормальний розподіл [або розподілена за нормальним законом (законом Гаусса)], якщо її густина
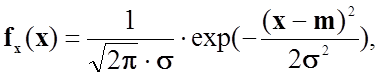 -∞<x<∞.
-∞<x<∞.
Ряд нормальних розподілів залежить від двох параметрів: m та σ.
Для того, щоб
побачити, яких значень набуває густина розподілу ймовірностей ![]() , при нульовому математичному очікуванні,
побудуємо графік розподілу за законом Гаусса в Mathcad.
, при нульовому математичному очікуванні,
побудуємо графік розподілу за законом Гаусса в Mathcad.
|
|
|
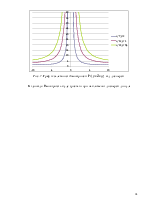
Рис. 6. Розподіл Гаусса |
|
|
Ймовірність влучення неперервної випадкової величини Х на ділянку від α до β визначається за формулою:
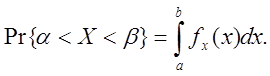
Підставимо задані за умовою значення: mx=0, σ
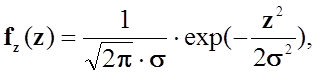
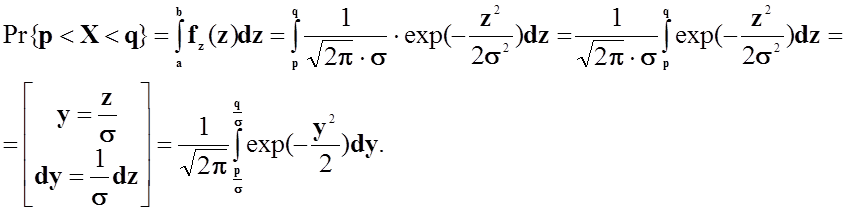
Для визначення екстремума функції, знайдемо похідну функції і прирівняємо її до 0.
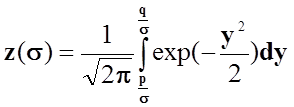 ;
;
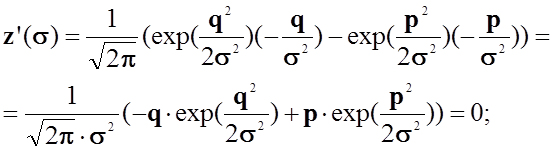
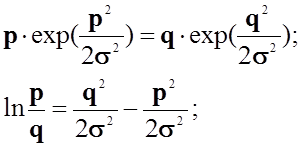
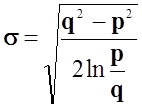 .
.
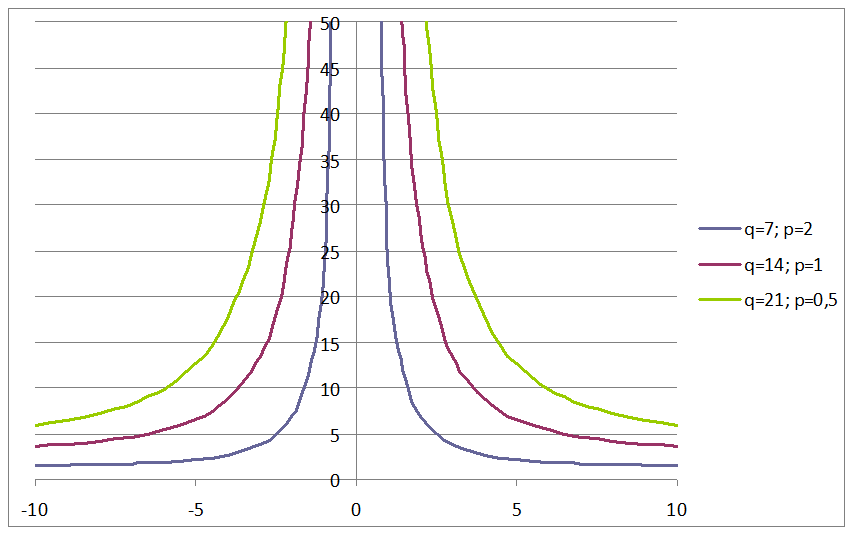
Рис. 7. Графік залежності ймовірності Pr{p![]() Z
Z![]() q} від дисперсії
q} від дисперсії
Відповідь: Ймовірність буде зростати при наближенні дисперсії до нуля
Знайти коефіцієнт ![]() ,
характеристичну функцію випадкової величини X, яка має густину розподілу
ймовірностей
,
характеристичну функцію випадкової величини X, яка має густину розподілу
ймовірностей
![]() ,
, ![]() ,
,
з заданими m – цілим та b – позитивним параметрами.
Густина f(x) будь-якої випадкової величини невід’ємна ( f(x) > 0) та має властивість:
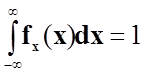 ,
,
тобто ймовірність повної групи подій дорівнює одиниці.
Отже, коефіцієнт визначимо за допомогою формули ймовірності для повної групи подій.
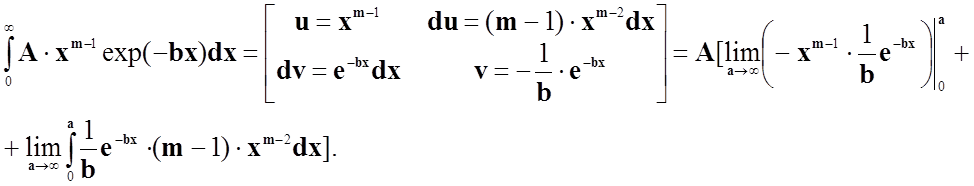 Використовуючи метод математичної
індукції, обчислимо заданий інтеграл:
Використовуючи метод математичної
індукції, обчислимо заданий інтеграл:
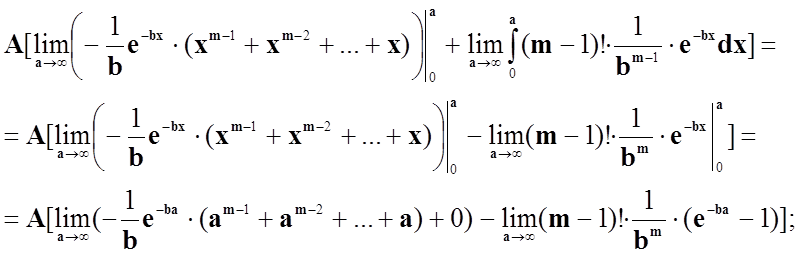
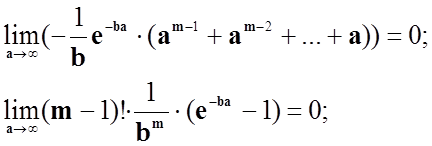
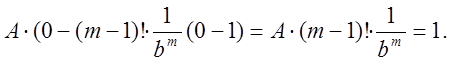
Знайдемо звідси А:
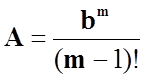 .
.
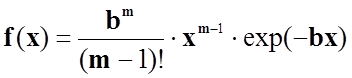 .
.
Характеристична функція має вигляд:
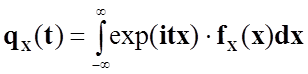 .
.
Підставимо в формулу нашу густину розподілу і знайдемо характеристичну функцію.
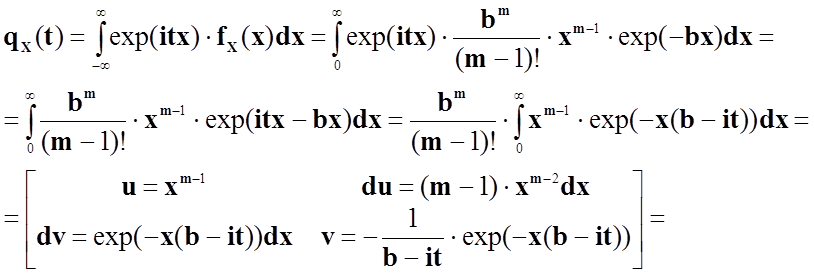
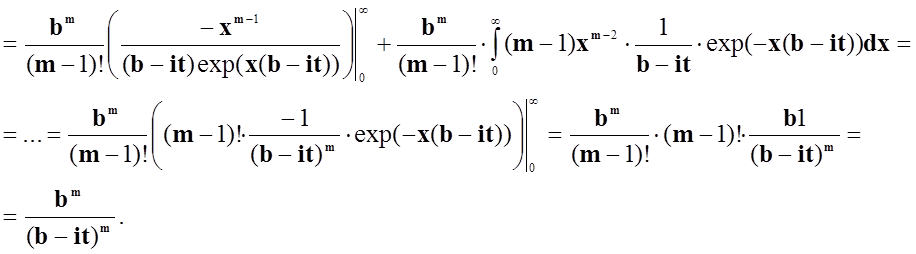
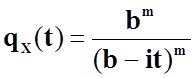 .
.
Відповідь:
коефіцієнт 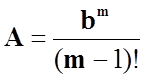 , характеристична функція має
вигляд
, характеристична функція має
вигляд 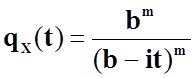 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.