



Павленко Наталія Ін-62
За моделями , знайденими за варіантами завдання 2 з таблиці 4 побудувати моделі з простором станів. Перевести систему зі стану Х0 у стан Х=0 (таблиця 7) за мінімальну кількість моментів часу.
|
88 |
(6,5,3) |
Модель вхід – вихід має вигляд
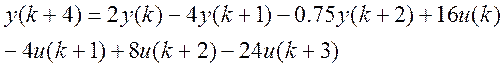
Задача полягає в тому, щоб створити закон керування який би за мінімальну кількість кроків на часовому проміжку [0,k] переводив би систему з х(0) =х0 в x(k)=k1, тобто з початкового стану в кінцевий.
Вважаємо систему повністю спостережувану та повністю керованою.
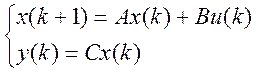 (1.1)
(1.1)
Нам дано ![]() , треба знайти
, треба знайти ![]() .
.
Для
спостережуваних систем розв’язок першого з рівнянь (1.1) має вигляд 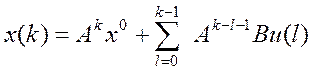 (1.2)
(1.2)
В (1.1) підставимо
к=0 і отримаємо ![]()
Треба знайти момент
часу ![]() такий, що стан системи
такий, що стан системи ![]() . З розв’язку рівняння (6.18) маємо:
. З розв’язку рівняння (6.18) маємо:
![]() (1.3)
– це є системою лінійних алгебраїчних рівнянь відносно керувань
(1.3)
– це є системою лінійних алгебраїчних рівнянь відносно керувань ![]() .
.
Систему 1.3
можно записати у вигляді ![]() (1.4)
, де
(1.4)
, де ![]() .
.
1.4 має єдиний
розв’язок за умови n=k
![]() - критерій Калмана.
- критерій Калмана.
![]() .
якщо
.
якщо ![]() то
то ![]()
Керування
системою повинно відбуватися за законом ![]() ,
тому ми маємо , що керування
,
тому ми маємо , що керування ![]() переводить
будь-який початковий стан
переводить
будь-який початковий стан ![]() в стан
в стан ![]() за
за ![]() кроків.
кроків.
![]()
![]()
![]()
моїй задачі
дана матриця 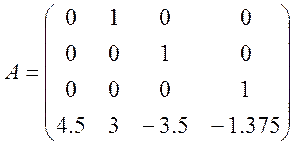
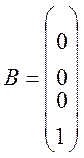
Нам потрібно
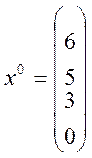 перевести до
перевести до 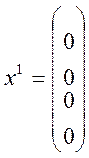
n=4, ![]()
![]() четвертий порядок матриці
четвертий порядок матриці 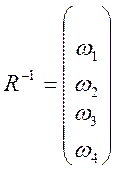 тобто
тобто ![]()
![]()
![]()
![]()
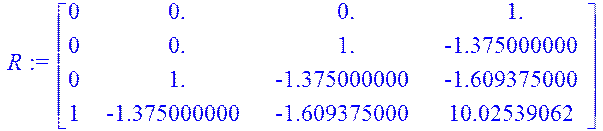
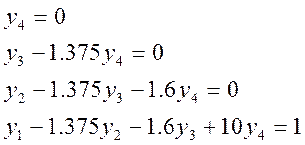
![]()
Потім ми
знаходимо ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
> with(linalg):with(LinearAlgebra):
A:=<<0|1|0|0>,<0|0|1|0>,<0|0|0|1>,<4.5|3|-3.5|-1.375>>;

> B:=<0,0,0,1>;

> X0:=<6,5,3,0>;
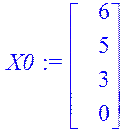
> AA:=A.A;
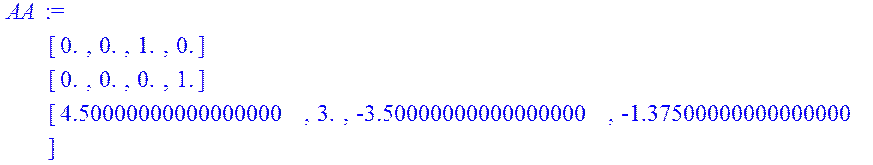
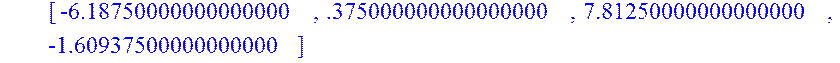
> AAA:=AA.A;
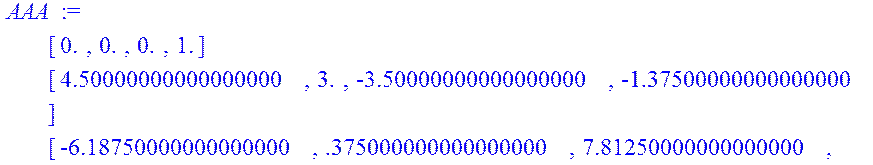
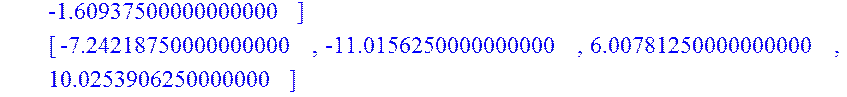
> AB:=A.B;
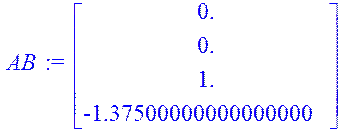
> AAB:=AA.B;
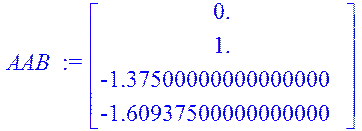
> AAAB:=AAA.B;
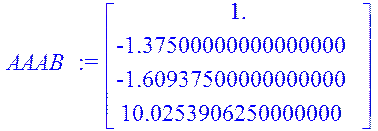
> R:=augment(B,AB,AAB,AAAB);
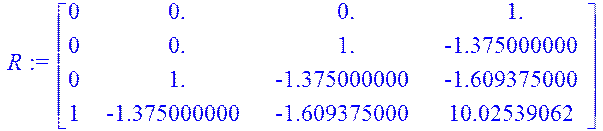
> W4:=<1|0|0|0>;
![]()
> A4:=AAA.A;
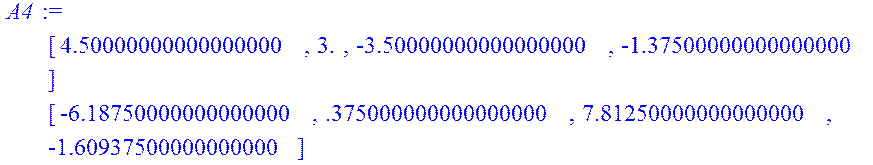
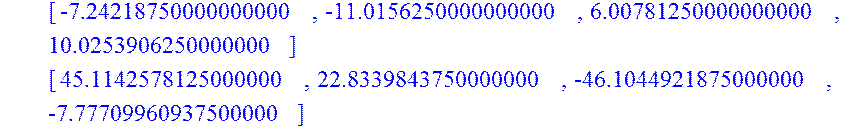
> F(x):=-W4.A4.X0;
![]()
> X1:=A.X0+B.F(x);
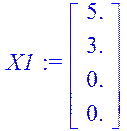
> F(x1):=-W4.A4.X1;
![]()
> X2:=A.X1+B.F(x1);

> F(x2):=-W4.A4.X2;
![]()
> X3:=A.X2+B.F(x2);
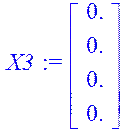
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.