3. Необходимые условия экстремума для функционала в задаче Лагранжа.
Прежде чем сформулировать необходимые условия в задаче (4.1) — (4.3), предположим, что уравнения (4.3), т.е. gj(x,y,y’)=0,j=1..k, k>n входящие в условия связи, независимы, т.е.
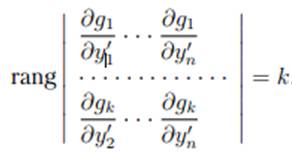
Введем в рассмотрение функциюF(x,y,y’ ,λ(x))=f(x,y,y’)+![]() . Эта
функция называется функцией Лагранжа, а λj(x) —
множителями Лагранжа. Тогда функционал
. Эта
функция называется функцией Лагранжа, а λj(x) —
множителями Лагранжа. Тогда функционал ![]() называется
вспомогательным функционалом и справедлива следующая теорема:
называется
вспомогательным функционалом и справедлива следующая теорема:
Теорема 2.1.Если
вектор-функция ![]() из С1
[a,b] является решением задачи
из С1
[a,b] является решением задачи
(4.1) — (4.3) и при этом выполнено условие (4.5), то
существуют такие функции ![]() что y*(x) является экстремумом функционала
что y*(x) является экстремумом функционала ![]() .
.
Определение 2.1. Экстремалями задачи Лагранжа называются экстремали функционала (4.1), удовлетворяющие граничным (краевым) условиям и дифференциальным связям.
Теорема фактически утверждает, все экстремали Лагранжа находятся среди экстремалей вспомогательного функционала. Значит, чтобы найти их, нужно из экстремалей вспомогательного функционала выбрать те, которые удовлетворяют условиям (4.2) и (4.3), т.е. краевым условиям и дифференциальным связям. Учитывая сказанное из теоремы 2.1. легко получить полную систему условий для экстремалей задачи Лагранжа.
Действительно, для отыскания n+k
неизвестных функций ![]()
![]() мы имеем n
уравнений Эйлера
мы имеем n
уравнений Эйлера![]() и k
уравнений связи
и k
уравнений связи ![]()
Среди решений выбираем те, которые удовлетворяют краевым условиям, которые в свою очередь не
должны противоречить условиям связи.
Замечание 2.3. К задаче Лагранжа можно свести задачу об экстремуме функционала вида
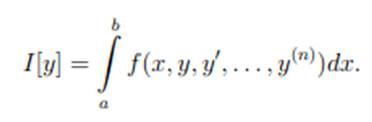
С этой целью введем новые функции y0=y, y1=y’,…,yn=y(n). Тогда исходный функционал примет вид
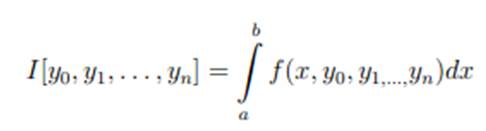
неизвестные функции в котором связаны уравнениями
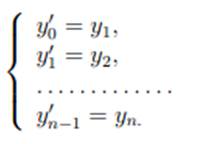
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.