 Министерство
образования Российской Федерации
Министерство
образования Российской Федерации
Рыбинская государственная авиационная технологическая академия имени П. А. Соловьева
Кафедра радиоэлектронных и телекоммуникационных систем
КИРИЛЛИН А. Н.
Спектральный анализ
пеРиодических сигналов
Методические указания
к лабораторной работе по дисциплине
"Основы радиоэлектроники и связи"
Рыбинск
2002
Цель работы – изучение методов спектрального анализа периодических сигналов, исследование амплитудного и фазового спектров периодических последовательностей прямоугольных, треугольных и косинусоидальных импульсов.
1.1 Краткие теоретические сведения
Для анализа и синтеза сигналов очень важны методы представления математической модели сигнала в виде обобщенного ряда Фурье по ортогональным базисным функциям.
Система функций ![]() , определенных на интервале времени
, определенных на интервале времени ![]() , называется ортогональной, если
скалярное произведение любых двух функций
, называется ортогональной, если
скалярное произведение любых двух функций ![]() и
и
![]() из этой системы удовлетворяет
условию
из этой системы удовлетворяет
условию
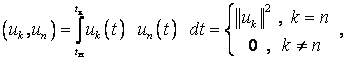 (1.1)
(1.1)
где 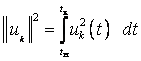 – квадрат нормы функции (для сигнала
– энергия).
– квадрат нормы функции (для сигнала
– энергия).
Такая система функций может быть использована в
качестве координатного базиса при представлении сигнала ![]() ,
определенного на интервале времени
,
определенного на интервале времени ![]() , в виде
обобщенного ряда Фурье
, в виде
обобщенного ряда Фурье
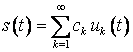 , (1.2)
, (1.2)
где 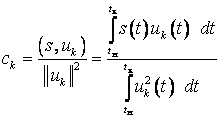 – коэффициент обобщенного ряда
Фурье.
– коэффициент обобщенного ряда
Фурье.
Разложение (1.2) существует, если на интервале
времени ![]() сигнал
сигнал ![]() удовлетворяет
условиям Дирихле:
удовлетворяет
условиям Дирихле:
– не имеет разрывов второго рода (с уходящими в бесконечность ветвями функции);
– имеет конечное число разрывов первого рода;
– имеет конечное число экстремумов.
Следует отметить, что вне интервала времени ![]() равенство (1.2) может не
выполняться.
равенство (1.2) может не
выполняться.
В настоящее время известно большое число ортогональных систем базисных функций: тригонометрические (гармонические) функции кратных аргументов, полиномы Эрмита, Лежандра, Чебышева, функции Бесселя, Лагерра, Хаара, Уолша и другие. Для анализа целесообразно выбирать систему функций, обеспечивающую наиболее быструю сходимость ряда Фурье , т.е. требующую наименьшего числа членов ряда для заданной точности представления сигнала.
В радиотехнике в качестве базисных функций чаще всего используют гармонические функции. Это связано с тем, что, во-первых, гармонический сигнал является единственным сигналом, сохраняющим свою форму при прохождении через стационарную линейную цепь (входной и выходной сигналы имеют одинаковую частоту, а отличаются амплитудой и/или начальной фазой), во-вторых, для анализа прохождения гармонических сигналов через линейные цепи разработан метод комплексных амплитуд, применение которого упрощает решение задачи.
Гармонические функции являются периодическими,
поэтому периодический сигнал ![]() , определенный на
бесконечном интервале
, определенный на
бесконечном интервале ![]() и удовлетворяющий условиям
Дирихле, может быть представлен в виде тригонометрического ряда Фурье
и удовлетворяющий условиям
Дирихле, может быть представлен в виде тригонометрического ряда Фурье
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.