Спектральный анализ периодических сигналов (лабораторная работа), страница 3

Коэффициенты комплексного ряда Фурье однозначно связаны с коэффициентами тригонометрического ряда Фурье

.

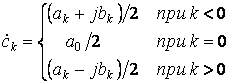Это означает, что тригонометрический и комплексный ряды Фурье можно рассматривать как два способа представления одного и того же ряда. Различие состоит в том, что в комплексном ряду в рассмотрение вводятся составляющие с отрицательными частотами. В результате постоянная составляющая сохраняет свое значение, а гармоническая составляющая распадается на две составляющие с одинаковыми, но уменьшенными в два раза амплитудами и одинаковыми по модулю, но противоположными по знаку частотами и начальными фазами.

Пример. Найдите спектр периодической последовательности прямоугольных импульсов положительной полярности, являющейся четной функцией времени, если амплитуда импульса равна U, длительность – , а период – Т.

Решение.

На интервале времени , равном периоду, заданную последовательность представим в виде

.

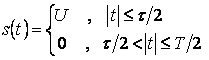Разложим сигнал в тригонометрический ряд Фурье. Данный периодический сигнал является четной функцией времени, поэтому  для всех значений , т.е. спектр содержит только косинусоидальные составляющие. Коэффициент ряда

.

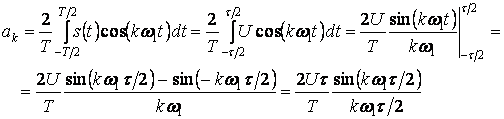Но основная частота , а скважность последовательности импульсов . Тогда

.

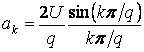Постоянная составляющая

.

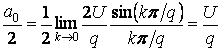Окончательно будем иметь

.

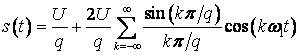Все коэффициенты ряда являются вещественными, поэтому амплитудный спектр образуется абсолютными значениями коэффициентов:

,

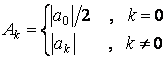а при нахождении фазового спектра следует иметь в виду, что каждая смена знака в последовательности коэффициентов приводит к скачку фазы на . Следовательно, фазовый спектр имеет ступенчатый характер, причем на частотах с положительными коэффициентами ряда фаза равна 0 (содержит четное число ), а на частотах с отрицательными коэффициентами –  (нечетное число ).

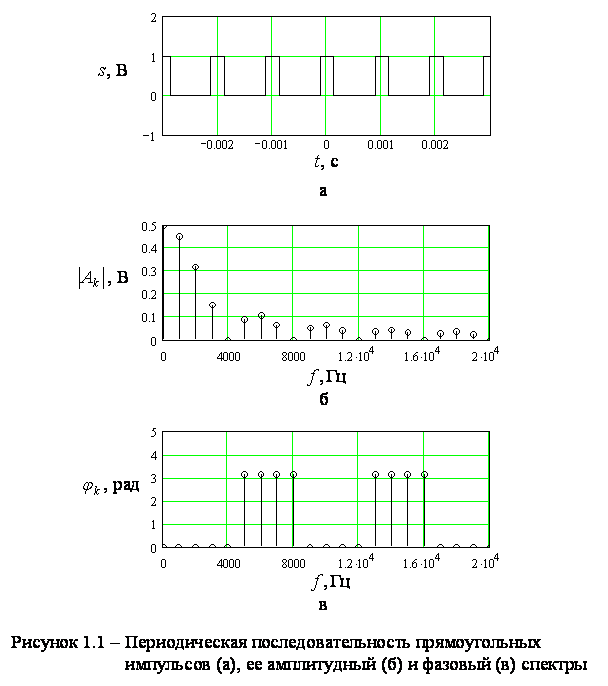
На рисунке 1.1 приведены периодическая последовательность прямоугольных импульсов, ее амплитудный и фазовый спектры при ,  и .

 

1.2 Домашнее задание

1.  Изучите указанную литературу.

2.  Найдите спектры периодических последовательностей импульсов, приведенных на рисунке 1.2.

3.  Ознакомьтесь с порядком проведения работы.

4.  Подготовьте ответы на контрольные вопросы.