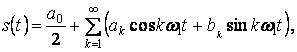Спектральный анализ периодических сигналов (лабораторная работа), страница 2

                                                 (1.3)

где – частота основной (первой) гармоники сигнала;

Т – период сигнала;

;

.

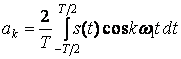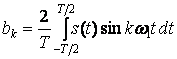Из (1.3) видно, что сигнал содержит независящую от времени постоянную составляющую  и бесконечное число гармонических составляющих (гармоник) с частотами , кратными частоте основной (первой) гармоники. При записи ряда Фурье в виде (1.3) каждая гармоника содержит косинусоидальную и синусоидальную составляющие. Обозначив в (1.3)  и , можно получить другую форму записи ряда Фурье

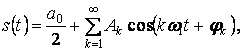                                                           (1.4)

где  – амплитуда k-ой гармоники;

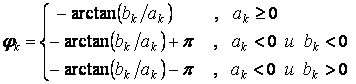– начальная фаза гармоники.

Множество амплитуд  образует амплитудный спектр сигнала, а множество начальных фаз  – фазовый спектр сигнала. Графически амплитудный и фазовый спектры изображают вертикальными отрезками на дискретных частотах . Длина отрезка пропорциональна амплитуде или фазе соответствующей гармоники.

Спектр периодического сигнала отличен от нуля только на частотах, кратных частоте первой гармоники , поэтому называется дискретным или линейчатым. Интервал между соседними составляющими спектра равен частоте первой гармоники, т.е. определяется периодом сигнала.

Если сигнал является четной функцией времени, то все коэффициенты  равны нулю, амплитуды гармоник , а начальные фазы  при  и  при . Если сигнал является нечетной функцией времени, то все , , а  при  и  при .

Спектральный анализ периодических сигналов становится более удобным, если в качестве ортогонального базиса взять систему комплексных экспоненциальных функций . В этом случае сигнал представляется комплексным рядом Фурье

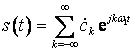,                                                                                (1.5)

где .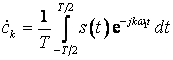

В соответствии с таким представлением спектр содержит компоненты как с положительными , так и с отрицательными  частотами. Коэффициенты ряда  являются комплексными, причем  и  отличаются только знаками мнимой части, т.е. являются сопряженными. Из сопряженности коэффициентов  и  следует, что амплитудный спектр (множество модулей коэффициентов ) является четной функцией, а фазовый спектр (множество аргументов ) – нечетной функцией частоты.