Линейную фильтрацию широко используют в системах передачи информации для обработки сигналов. Объясняется это прежде всего простотой реализации линейных фильтров, которые легко синтезируются и существованием развитой теории их построения.
Линейные фильтры являются: неотъемлемой частью любого приемного устройства. С их помощью осуществляется как додетекторная, так и последетекторная обработки сигналов. С помощью лишенных фильтров сигналы разделяются в многоканальных системах передачи. Рассмотрим теорию оптимальной линейной фильтрации.
Пусть сигнал на входе линейного фильтра с
импульсной реакцией g(t) представляет сумму
переданного сигнала s[t) и помехи п(t)![]()
Требуется найти такую функцию g(t)
![]()
где s^(t)—оценка сигнала на выходе фильтра. Время запаздывания сигнала s^(t) в фильтре t0=0, а среднее значение берется по ансамблям сигналов S и помех N. Будем полагать, что s(t) и n(t) — стационарные взаимно-некоррелированные процессы с известными энергетическими спектрами Gs(f) и GN(f).
импульсная реакция фильтра должна удовлетворять условию g(t)=0 для всех t<0. Этп ограничение учитывается в записи
![]()
|
|
где область интегрирования γ для физически реализуемого фильтра есть интервал (0,∞), а для нереализуемых фильтров - (-∞, о). Можно доказать, что Необходимым и достаточным условием оптимальной линейной фильтрации является условие (1)
Это означает, что фильтр нужно выбрать так, чтобы ошибка g(t)=s^(t)-S(t) была не коррелированна со входным сигналом Z(t) со всe моменты времени в области у. Докажем справедливость условии. Пусть g1(t)—импульсная характеристика оптимального фильтра, удовлетворяющего условию (7.60), g2(t)—импульсная характеристика любого другого линейного фильтра. Отклики фильтров S1(t) и S2(t). Тогда
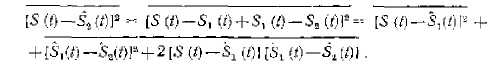
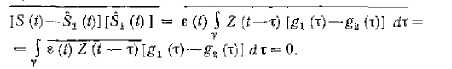
![]()
это выражение будет минимальным, при S1(t) =S2(t) что доказывает справедливость условия (1). Смысл этого условия состоит в том, что случайный вектор S должен быть строго ортогональной
проекцией S на линейное
подпространство, порождаемое случайным вектором z. Представим условие (1) ![]() для всех τ и γ. Отсюда
для всех τ и γ. Отсюда
![]()
или![]() (2)
(2)
когда сигнал S (t) и помеха n(t) некоррелированы (2) принимает вид
![]() (3)
(3)
Это основное интегральное уравнение теории линейной фильтрации называется уравнением Винера — Хопфа. Его решением является искомая: функция g(t), минимизирующая средний квадрат ошибок
Уравнение (3) легко решается для нереализуемых фильтров, т. е. когда γ=(-∞,∞). Отсюда, коэффициент передачи оптимального линейного фильтра
![]()
или в более общем случае, когда учитывается время запаздывания
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.