Дослідження на керованість, спостережуваність та асимптотичну стійкість дискретних моделей з простором станів (Лабораторна робота № 5)

Лабораторна робота № 5

Берко А.М.

Варіант № 7

Завдання.  Дискретні моделі з простором станів, отримані в завданні 3 дослідити на керованість, спостережуваність та асимптотичну стійкість.

Дискретна модель з простором станів:

 

 

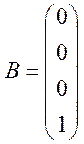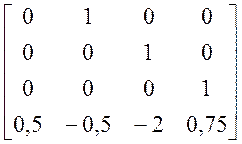
Дослідимо систему на керованість. Вона стаціонарна тому використаємо критерій Калмана, перевіримо умову rg(B, АВ,..., А^n-1B) = n, n=4. Використаємо пакет Maple:
> restart:

with(linalg):

with(LinearAlgebra):

A:=<<0|1|0|0>,<0|0|1|0>,<0|0|0|1>,<0.5|-0.5|-2|0.75>>;

B:=<<0,0,0,1>>;

AB:=Multiply(A,B);                                                                                            A2:=Multiply(A,A);                                                                                                                              A2B:=Multiply(A2,B);A3:=Multiply(A2,A);                                                                                    A3B:=Multiply(A3,B);                                                                                    K:=augment(B,AB,A2B,A3B);

rank(K);

 

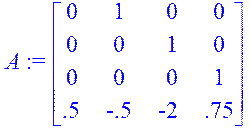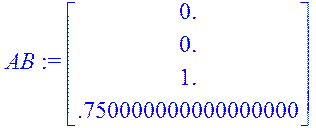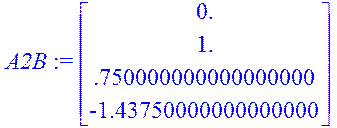
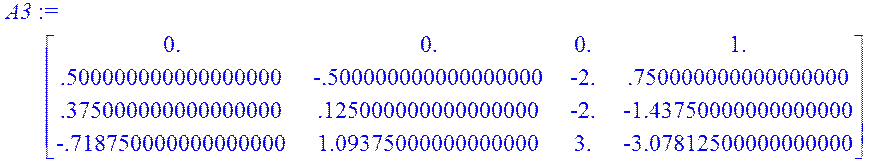
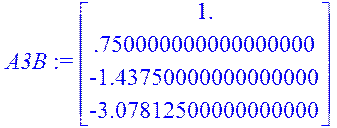
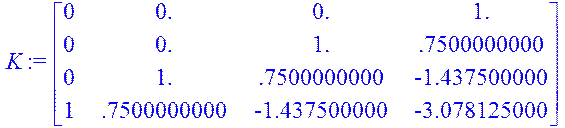
Формувати необхідну поведінку системи - це означає описати умови, які повинні задовольняти або процес y(k), або x(k), і знайти таке керування u(k), що завдяки рівнянням (5.1), (5.2) забезпечує виконання цих умов.

Розглянемо двоточкову граничну задачу керування. Задано стани x⁰, x¹ і моменти часу k₀ і k₁. Потрібно знайти таке керування на інтервалі часу [k₀, k₁], що переводить подію (k₀, x⁰) у подію (k₁, x₁) по траєкторії системи (5.1).

З'ясуємо, коли ця задача має Розв’язання. Для цього, користуючись формулою загального розв’язку різницевого рівняння , випишемо умову x(k₁) = x¹, а саме:

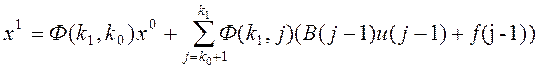 . (5.3). Отже, керування u(k), що розв’язує двоточкову граничну задачу, повинно забезпечити виконання рівності

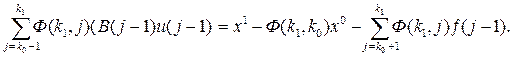
Критерій Калмана виконується, тому система повністю керована.

Система (5.1) називається k₁-досяжною, якщо для будь-якого стану x^l існують k₀=k₀(x¹) > -∞ і таке керування, яке переводить систему із стану x⁰ = 0 у x¹. Для одержання умов k₁ -досяжності варто розглянути питання можливості розв'язання системи (5.4) при x⁰ = 0 і будь-якому х¹. У цьому випадку v(k₀, k₁) може бути довільним вектором у Rⁿ, тому (5.6) стає необхідною і достатньою умовою можливості розв'язання цієї задачі.

Теорема . Система (5.1) повністю k₁-досяжна тоді і тільки тоді, коли існує k₀ > - ∞ і виконується умова (5.6).

Для стаціонарних систем для повної досяжності необхідно і достатньо виконання умови (5.10).

Якщо матриця А - невироджена, то (5.10) також є необхідною і достатньою умовою повної керованості.

Можна показати, що якщо rgА= m, то критерієм повної досяжності є

rg(B,AB,...,A^n-mB) = n.                               (5.12)

Задача виявлення (оцінювання) стану х⁰ на основі даних u[k₀, k₁] і y[k₀, k₁] називається задачею спостереження, а виявлення стану x¹ - задачею діагностики.

Розглянута система є нестаціонарною, закон її поведінки, що виражається матрицями A(k),B(k) і C(k), змінюється за часом, і розв’язання зазначених задач залежать від інтервалу спостереження [k₀, k₁]. Тому доцільно першу задачу називати задачею k₀-спостереження, а другу k₁-діагностики.

Розглянемо питання про можливість розв'язання задачі k₀-спостереження.

Становлять інтерес умови на матриці A(k), B(k) і C(k), що забезпечують можливість розв'язання зазначених задач.

Спочатку розглянемо випадок, коли u[k₀, k₁] = 0 і ƒ(k) = 0.

Нехай х⁰ - невідомий стан у момент k₀ і y[k₀, k₁] - відповідний йому вихід. Оскільки y[k₀,k₁] може породжуватися й іншими початковими станами х, то множину усіх таких х позначимо через Q(x⁰,k₀,k₁). Множина Q(x⁰,k₀,k₁)  є площиною в Rⁿ. Дійсно, згідно з (5.1) і (5.2) кожен стан х^*  Q(x°, k₀, k₁) задовольняє систему рівнянь

           C(k₀)x^* = y(k₀),

                       C(k₀+1)Ф(k₀+1, k₀)x^* = y(k₀+1),

                            ………………………………………     (5.13)