C(k0+k1)Ф(k0+k1, k0)x* = y(k0+k1).
Множина тих x, що задовольняють систему рівнянь (5.13), являє собою площину відповідної розмірності в Rn. Введемо позначення:
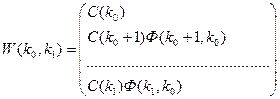 ,
,
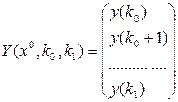 .
.
Тоді (5.13) перепишеться у вигляді
W(k0, k1)x* = Y(x0, k0, k1). (5.14)
Тепер дослідимо систему на спостережуваність.
Критерієм повної спостережуваності для стаціонарних систем має вигляд:
rg![]() = n
= n![]()
Нехай спочатку u[k0,k1]=0. Для стану, що реалізувався, х1=x(k1) завжди існує стан x0 , такий, що Ф(k1,k 0)x0 =x1. Якщо detФ(k1, k0) = 0, то існує єдиний x0, що дорівнює Ф-1(k1, k0)x1, що переходить на [k1, k0] у x1, і задача оцінювання x1 зводиться до оцінювання x0, тобто до задачі k0 - спостереження і обчислення x1 як х1= Ф(k1,k0)x0. Умова detФ(k1, k0) ≠ 0 виконується тоді і тільки тоді, коли detА(k)≠0 при всіх k=k0,..., k1. Отже, у випадку detA(k)≠0 система (5.1), (5.2) повністю k1 - досяжна тоді і тільки тоді, коли вона повністю k0-спостережувана, і критерієм цього є умова (5.15), а для стаціонарних систем - умова (5.20).
У випадку detA(k)≠0 з повної k0-спостережуваності також випливає можливість оцінити стан x1, оскільки при відомому x(k0) однозначно знаходимо x1 = Ф(k1, k0)x(k0).
Зауважимо, що в задачах k1-діагностики та k0 – спостережуваності потрібно виявити стан в один і той самий момент k1. Однак можливість розв'язання однієї з них необов'язково дає можливість розв'язати іншу. Разом з тим, для стаціонарних систем за умови detA≠0 ці задачі еквівалентні, і далі будемо в обох випадках говорити про них як про задачу спостереження.
Випадок u[k0,k1]≠0 аналізується аналогічно.
Перевіримо цю умову за допомогою пакета Maple:
> C:=<<0.203|0.875|0.125|0.281>>;
CA:=evalm(C&*A);
CA2:=evalm(C&*A2);
CA3:=evalm(C&*A3);GG:=stackmatrix(C,CA,CA2,CA3);
rank(GG);
![]()
![]()
![]()
![]()

![]()
Необхідна умова виконується, тому система є повністю спостестережуваною.
Дослідимо систему наасимптотичну стійкість. Рух кожного об'єкта описується системою n диференціальних рівнянь (5.21) першого порядку, записаних у нормальній формі:
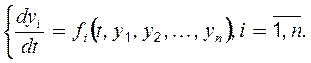 (5.42)
(5.42)
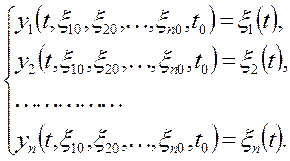 У системі (5.42) невідомими є
функції часу
У системі (5.42) невідомими є
функції часу ![]()
![]() , у системах (5.43) і
(5.44) —
, у системах (5.43) і
(5.44) — ![]() і
і ![]() . Нехай
функції
. Нехай
функції ![]() визначені в n - вимірній кулі
радіуса
визначені в n - вимірній кулі
радіуса ![]() для
для ![]() і
задовольняють там деякі умови, що гарантують існування неперервно
диференційованих
і
задовольняють там деякі умови, що гарантують існування неперервно
диференційованих ![]() , що є розв’язком системи (5.42).
Доповнимо систему (5.42) початковими умовами. При
, що є розв’язком системи (5.42).
Доповнимо систему (5.42) початковими умовами. При ![]() існує
набір чисел
існує
набір чисел ![]() , узятих з n -вимірної кулі
, узятих з n -вимірної кулі ![]() , що дозволяє єдиним способом одержати c1,
c2, …, cn . Функції
, що дозволяє єдиним способом одержати c1,
c2, …, cn . Функції ![]() при
цьому переходять у єдину систему часткових розв’язків системи (5.42):
при
цьому переходять у єдину систему часткових розв’язків системи (5.42):
Надалі доведеться змінювати початкові умови і
відповідно часткові розв’язки. При цьому припускаємо, що ці зміни не виводять
функції ![]() і початкові умови з області визначення
правої частини рівнянь (5.42). Дамо визначення стійкості розв’язку системи
(5.42). Нехай відомий частковий розв’язок системи (5.42)
і початкові умови з області визначення
правої частини рівнянь (5.42). Дамо визначення стійкості розв’язку системи
(5.42). Нехай відомий частковий розв’язок системи (5.42) ![]() , що відповідає початковим умовам при
, що відповідає початковим умовам при ![]()
![]() ,
, ![]() . Змінимо початкові умови при
. Змінимо початкові умови при ![]()
![]() . Часткові розв’язки,
що відповідають цим новим умовам, позначимо
. Часткові розв’язки,
що відповідають цим новим умовам, позначимо ![]() .
Функції
.
Функції ![]() описують так званий незбурений розв’язок, а
описують так званий незбурений розв’язок, а ![]() - збурений
- збурений
Розв’язок ![]() системи (5.42) називається стійким за
Ляпуновим, якщо для
будь-якого заданого як завгодно малого додатного числа
системи (5.42) називається стійким за
Ляпуновим, якщо для
будь-якого заданого як завгодно малого додатного числа ![]() можна
визначити таке мале додатне число
можна
визначити таке мале додатне число ![]() , що при
, що при![]() (5.45), для всіх
(5.45), для всіх ![]() і
і
![]() виконується нерівність
виконується нерівність ![]() ,
, ![]() . (5.46).
Якщо при виконанні умов (5.45), (5.46) виконані ще умови
. (5.46).
Якщо при виконанні умов (5.45), (5.46) виконані ще умови![]() (5.47),для усіх
(5.47),для усіх ![]() , то розв’язок
називається асимптотично стійким
, то розв’язок
називається асимптотично стійким
За теоремою Ляпунова: Для асимптотичної стійкості системи (2) необхідно і достатньо, щоб модулі всіх власних чисел матриці А були менше одиниці.
Перевіримо чи виконуються умови теореми.
> with(LinearAlgebra):
AA:=<<0|1|0|0>,<0|0|1|0>,<0|0|0|1>,<0.5|-0.5|-2|0.75>>; Xa:=CharacteristicPolynomial(AA,lambda);
Specter:= solve ({Xa});
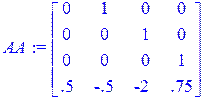 |
||||
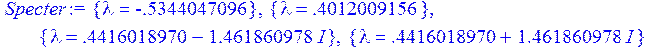 |
||||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.