Аппроксимация сигнала многочленом Фурье по ортогональной системе гармонических функций, страница 6

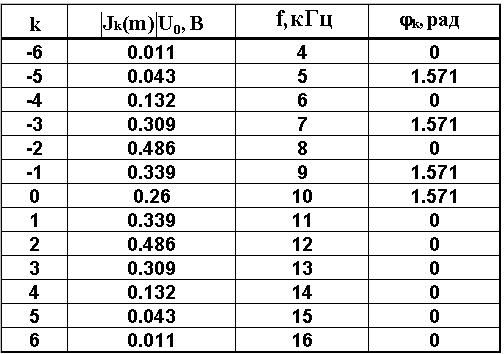
Таблица 4. Значения амплитуд  и начальных фаз  колебания  при тональной угловой модуляции (рис.8а.)

                 

7. Синтез сигнала с равномерным спектром.

Такой сигнал можно представить в виде

   .

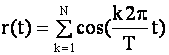У него все значения амплитуд гармоник равны 1В, а начальные фазы нулевые.

Если N®¥,  то исходный сигнал будет представлять собой последовательность дельта-функций:

.

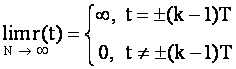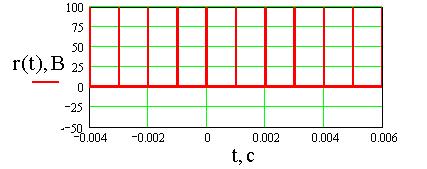
Рис.9. График сигнала с равномерным спектром при T= 1мс, N=100.

8. Схема формирования сигналов в пакете ElectronicsWorkbench и осциллограммы этих сигналов. 

                                           

Рис.10. Схема формирования сигналов

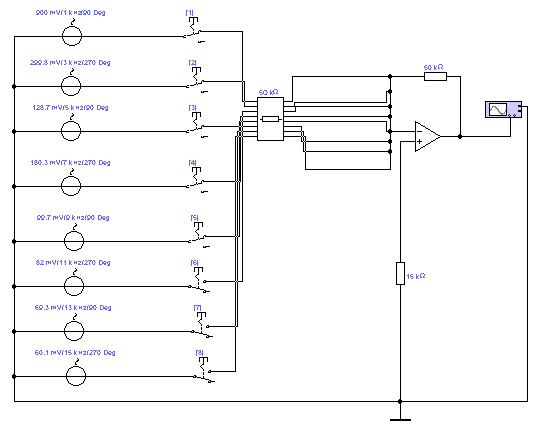
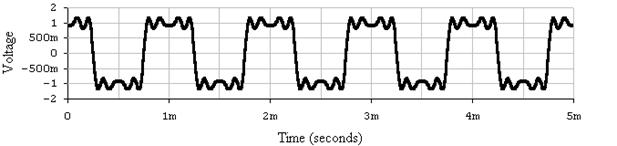
        а

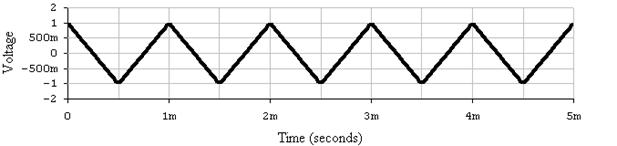
        б

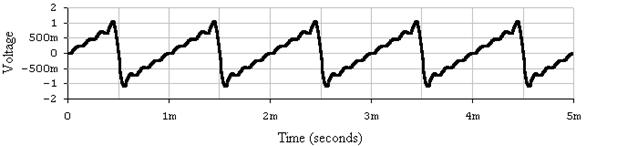
        в

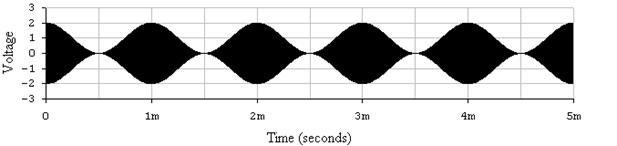
         г

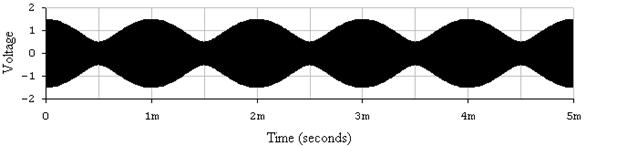
          д

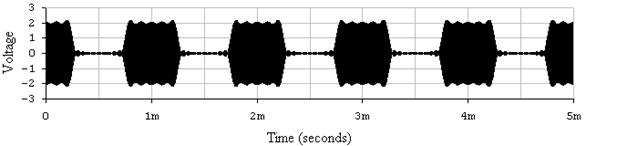
           е

            ж

Рис.11. Осциллограммы сигналов построенные в пакете ElectronicsWorkbench

9. Вывод.

1.  При увеличении числа гармоник среднеквадратическая погрешность аппроксимации периодических последовательностей видеоимпульсов уменьшается.

2.  При амплитудной модуляции огибающая несущего колебания изменяется по закону модулирующего сигнала, а фаза и частота остаются неизменными; коэффициент амплитудной модуляции M определяет степень относительного изменения огибающей, при экстремальных значениях модулирующего сигнала амплитуда колебания изменяется на M.

3.  При угловой модуляции полная фаза сигнала изменяется в соответствии с модулирующим сигналом; при однотональной угловой модуляции мгновенная частота сигнала  изменяется от  _min=- m до  _max=+m

4.  Сигнал с равномерным спектром 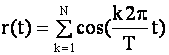стремится к  последовательности отстоящих друг от друга на T дельта-функций.