Аппроксимация сигнала многочленом Фурье по ортогональной системе гармонических функций, страница 3

      

                                                             а

                                                              б

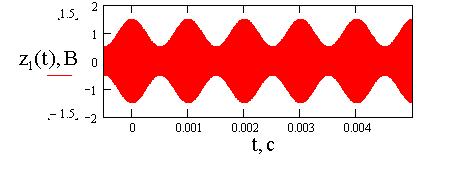
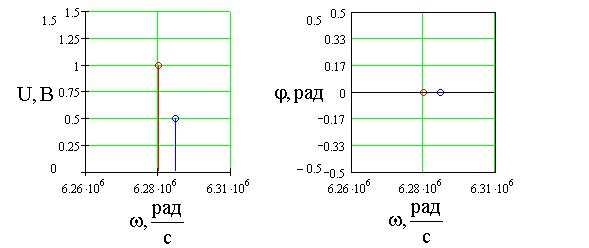
Рис.6. График однотонального АМ-сигнала с подавленной нижней боковой частотой (а) и его спектральная диаграмма (б) при = 1В, =2p10⁶ рад/с, = 2p10³, M=1, ==0.

4.  Нахождение спектров амплитуд и начальных фаз колебания при  модуляции периодической последовательностью импульсов, приведенной на рис.1а.

Такое колебание можно представить в виде

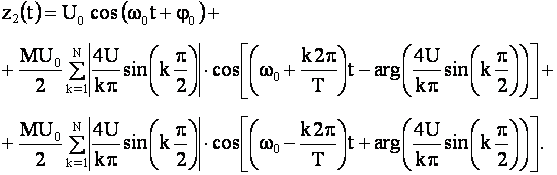
Таким образом, в спектре сложномодулированного АМ-сигнала, помимо несущего колебания, содержатся группы верхних и нижних боковых колебаний.

       

  а

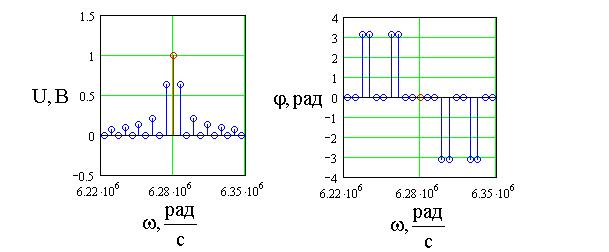    б

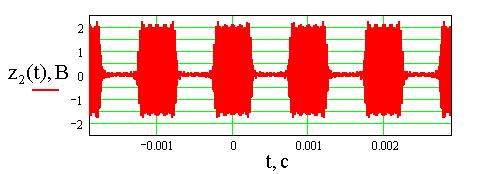
Рис.7. График сложномодулированного АМ-сигнала (а) и его спектральная диаграмма (б) при = 1В, =2p10⁶ рад/с, T= 1мс, M=1, N=10, =0.

5.  Нахождение спектров амплитуд и начальных фаз колебания с тональной  угловой модуляцией.

При гармонической угловой модуляции

 или

                     

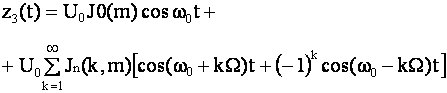
При такой модуляции спектр содержит бесконечное число боковых составляющих, частоты которых отличаются от частоты несущего колебания на величину, кратную частоте модулирующего колебания.

              

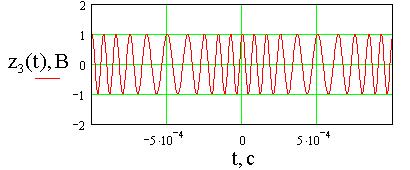
а

 

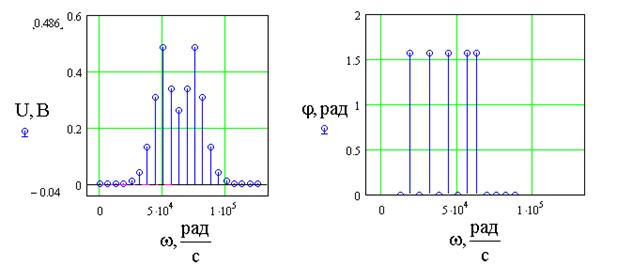
  б

Рис.8. График модулированного  колебания с тональной угловой модуляцией (а) и его спектральная диаграмма (б) при = 1В, =2p10⁴рад/с, = 2p10³, m=3.

6. Таблицы значений амплитуд и начальных фаз гармоник синтезируемых сигналов, рассчитанных в пакете Mathcad.

Таблица 1. Значения амплитуд Ak и начальных фаз фk гармоник сигнала представленного на рис.2а.

k	Ak, В	fk, кГц	фk,рад
1	1.273	1	0
2	0	2	0
3	0.424	3	3.142
4	0	4	3.142
5	0.255	5	0
6	0	6	0
7	0.182	7	3.142
8	0	8	3.142
9	0.141	9	0
10	0	10	0