Аппроксимация сигнала многочленом Фурье по ортогональной системе гармонических функций, страница 2

На рис.3. приведены аппроксимация    сигнала    , его амплитудный и фазовый спектры при   =1В, =1мс,  N=10.

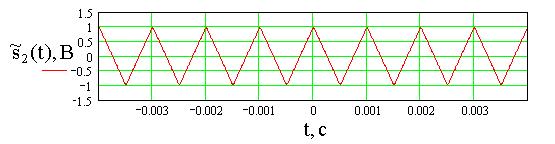
   а

  

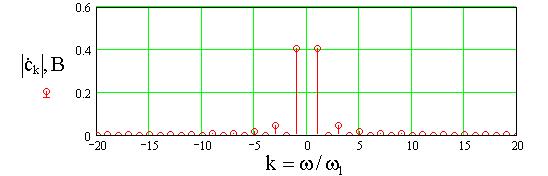
      б

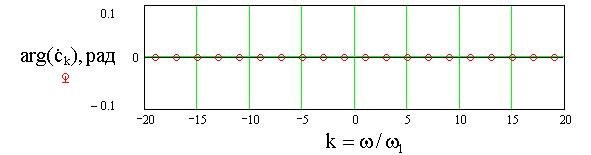
                            в

Рис.3. Аппроксимация    сигнала     (а), его амплитудный (б) и фазовый (в) спектры при U= 1В, T= 1мс, N=10.

На интервале времени [,], равном периоду, последовательность рис.1в. представим в виде

.

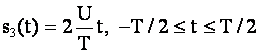Аппроксимация    сигнала        конечным    числом     членов  тригонометрического ряда Фурье  

      

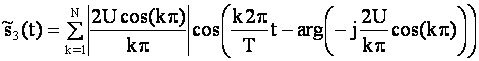
при N= 10, U= 1В, T= 1мс  даёт относительную погрешность

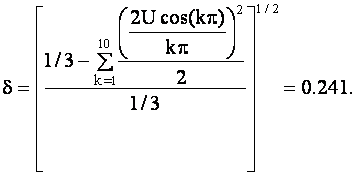
Коэффициенты комплексного ряда Фурье определяются равенством

.

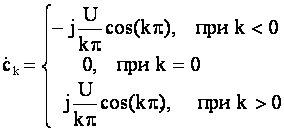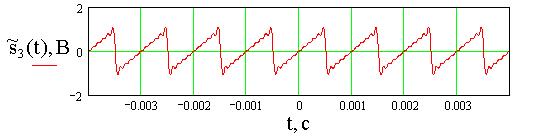
На рис.4. приведены аппроксимация    сигнала    , его амплитудный и фазовый спектры при   =1В, =1мс,  N=10

        

                а

        

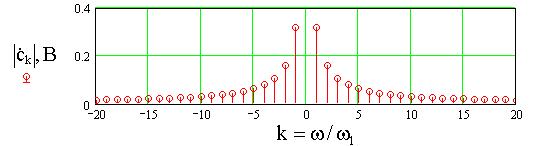
                  б

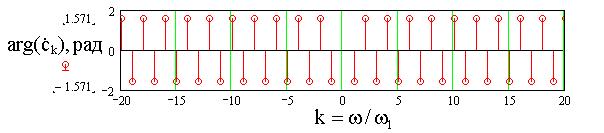
                 в

Рис.4. Аппроксимация    сигнала     (а), его амплитудный (б) и фазовый (в) спектры при U= 1В, T= 1мс, N=10.

2.  Нахождение спектров амплитуд и начальных фаз колебания с тональной  амплитудной модуляцией.

При тональной амплитудной модуляции модулированное  колебание можно представить в виде

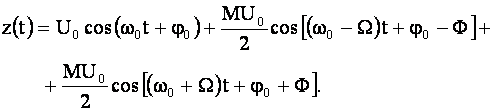
Спектр такого сигнала содержит три составляющие: 1)несущее колебание с частотой , 2) колебание нижней боковой частоты , 3) колебание верхней боковой частоты .

                     

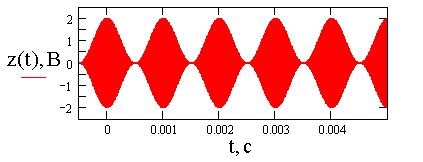
           а

            

           б

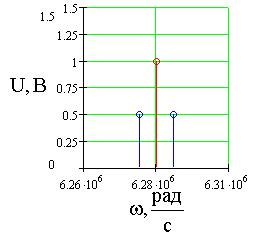
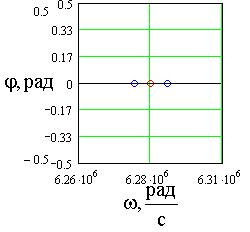
Рис.5. График модулированного  колебания с тональной амплитудной модуляцией (а) и его спектральная диаграмма (б) при = 1В, =2p10⁶ рад/с, = 2p10³, M=1, ==0.

 3.  Нахождение спектров амплитуд и начальных фаз колебания с однополосной тональной  амплитудной модуляцией.

Рассмотрим однотональный АМ-сигнал с подавленной нижней боковой частотой

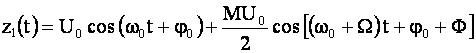
Спектр такого сигнала содержит две составляющие: 1)несущее колебание с частотой , 2) колебание верхней боковой частоты .