Оцінка складністі алгоритмів факторизації. Факторизація Ферма (Практичне заняття № 3)

Практичне заняття №3 (ТСО).

 Мета заняття : Поглибити теоретичні знання і навчитися на практиці оцінювати складність алгоритмів факторизації.

 Факторизація Ферма.

 Вельми плідною ідеєю при побудові алгоритмів факторизації є пошук чисел   і , для яких виконується співвідношення . Якщо при цьому , то числа   і   суть нетривіальні дільники числа

 Очевидно, першим в цьому напрямі є метод факторизації, застосований

П. Ферма. Він заснований на теоремі Ейлера про представлення числа у вигляді різниці двох квадратів.

 Теорема. Якщо  - непарний, то існує взаємно однозначна відповідність між розкладаннями на множники ,   і представлені у вигляді різниці квадратів , . Ця відповідність має вигляд

 

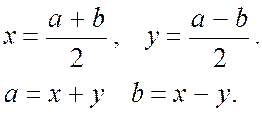
 Доказ очевидно.

 

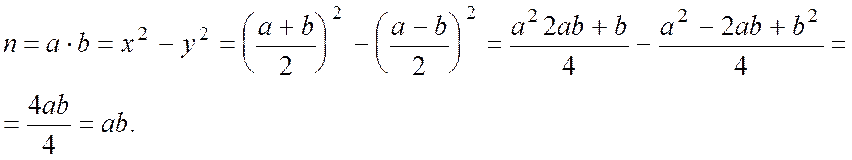
 Метод Ферма полягає в тому, що при малих значеннях параметра  в уявленні   можна знайти пару , перебираючи як кандидатів на значення числа   числа 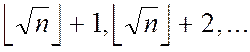  і перевіряючи для кожного з них рівність

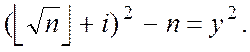
 Для отбраковки помилкових значень  можна скористатися тим, що якщо число не є квадратом, то воно з великою вірогідністю не буде і квадратичним лишком для одного з невеликих простих чисел  Остання властивість легко перевіряється шляхом обчислення відповідного символу Лежандра.

 Вхід:   непарне число,  невеликі прості числа.

 Крок 0. Перевірити  Якщо так, то дільник знайдений.

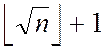 Крок 1. Для кожного    від  до 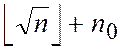   обчислити величини

 Крок 2. Якщо хоч би для одного   виконано одну з умов:

  і   не ділить   або

   і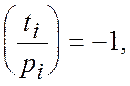

 то перейти до наступного  на кроці 1. В протилежному випадку перейти до кроку 3.

 Крок 3. Перевірити, чи  є повним квадратом. Якщо   то видати відповідь: «складене».

 Якщо  - не повний квадрат, то перейти до наступного   на кроці 1.

 Наприклад

 Хай потрібно факторизувати число   Вхід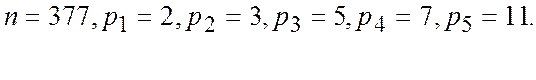

 Крок 0. 377 не ділиться на жодне

 Крок 1.

             .

            

            

            

             ...

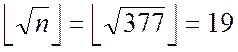
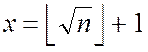
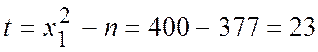
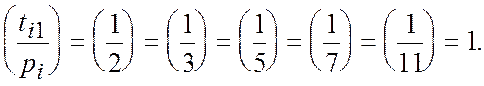                        (т.я.  );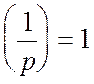

                            

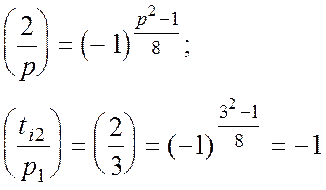
 Виконано умову   і 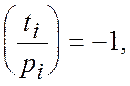  переходимо до наступного  

                                

                          ( , але   ділить )

                        ;

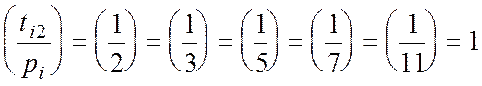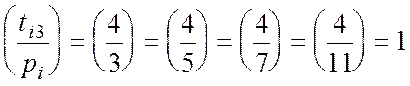                        ( т.к. );

                         

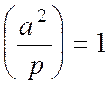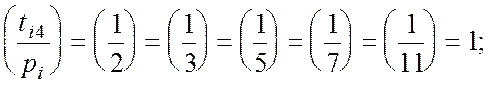
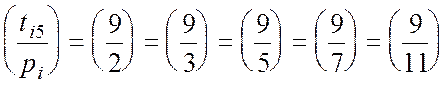                         =1.

 Умови   і   не ділить   або

                    і 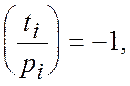 не виконуються для жодного

 Переходимо до кроку 3.

 Перевіряємо, чи   є повним квадратом

=8²                                

  - складене 

 По суті даний алгоритм, подібно до методу „пробних ділень”, є різновидом методу перебору всіх можливих дільників. Складність цього алгоритму оцінюється величиною . Параметр  визначається з конкретних обчислювальних можливостей. Чим більше значення , тим більше число можливих дільників буде перевірено. Проте, на відміну від методу „пробних ділень”, за допомогою якого знаходиться найменший дільник, даний метод дозволяє знаходити найбільшого дільника числа, що не перевершує    

 Помітимо, що замість   можна брати   при малих значеннях

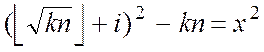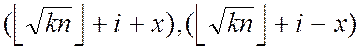 У багатьох випадках перехід до рівнянь , . дозволяє знайти шукане значення шляхом коротшого перебору значень , чим при . При цьому, у разі успіху таке уявлення також дозволяє факторізовать число , оскільки числа  лежать в інтервалі  і задовольняють рівності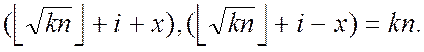

 Алгоритм Діксона.

 У багатьох сучасних алгоритмах факторизації для знаходження дільників використовується ідея Лежандра (1798 р.). що полягає в пошуку чисел   и , що задовольняють умовам

 Цей підхід є узагальненням методу Ферма, в якому потрібне виконання строгої рівності.

  Для пошуку таких чисел використовується поняття факторної бази.

 Назвемо факторною базою деяку множину  невеликих простих чисел. Звичайно в якості  беруть прості числа, що не перевершують деякої межі

 Говоритимемо, що ціле число   є - числом, якщо число   розкладається на добуток простих чисел з факторної бази.

 .

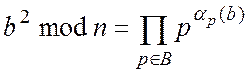 Зіставимо кожному - числу вектор показників з цього розкладання

 

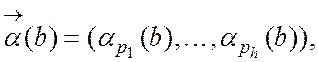
 а також двійковий вектор, одержаний з вектора 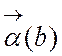  приведенням всіх його координат по модулю 2

 

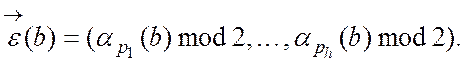
 Якщо тепер яким-небудь чином підібрати таке меножество різних - чисел ,  при якому виконується лінійне співвідношення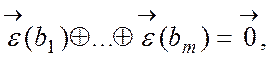

 то для добутку   виконується співвідношення

 

 де число  визначається по векторах показників рівністю

 

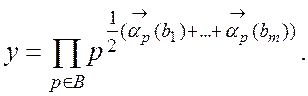
 Алгоритм Діксона полягає в наступному.

 Крок 1. Вибрати випадкове ,, і обчислити .

 Крок 2. Пробними діленнями спробувати розкласти  на прості множники з факторної бази.

 Крок 3. Якщо   є -числом, тобто ,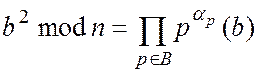

 то запам'ятати 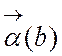  і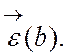 Повторити процедуру генерації чисел   до тих пір, поки не буде знайдено   - чисел .

 Крок 4. Знайти . наприклад, вирішуючи за допомогою алгоритму послідовного виключення невідомих Гауса однорідну систему лінійних рівнянь 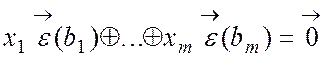 відносно невідомих  співвідношень лінійної залежності

,

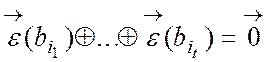 Покласти

 ,

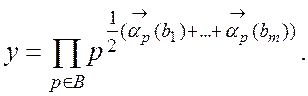
 Крок 5. Перевірити  Якщо це так, то повторити процедуру генерації. Якщо ні, то знайдено нетривіальне розкладання

 

 Приклад. Хай потрібне факторізовать число

 Хай   Фактор-база 2,3,5.

                             

       

3.

  

                                           

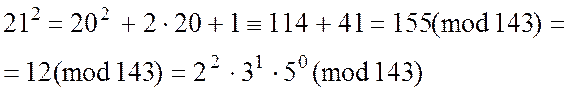
НСД

НСД

НСД

НСД

 На трудомісткість алгоритму Діксону істотно впливає вибір бази, чинника. Якщо число  вибране так, що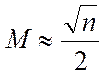, то майже кожне  буде -числом, але одержувані при цьому порівняння  будуть тривіальними. Крім того, потрібно буде вирішувати системи від дуже великого числа невідомих. Якщо   - мало, то   - числа з'являтимуться дуже рідко.

 Помітимо, що якщо   - складене, то рівняння    має принаймні 4 рішення. Тому вірогідність появи пари  з  не перевершує 1/2. Отже, повторюючи процедуру набору для отримання потрібної пари   разів ми одержимо, що надійність даного методу знаходження дільника не менша, ніж .

 Трудомісткість алгоритму  Діксону оцінюється таким чином:

 

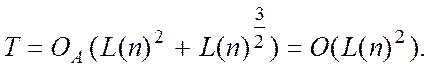
 Через   позначено