Оцінка складністі алгоритмів факторизації. Факторизація Ферма (Практичне заняття № 3), страница 2

 Алгоритм Діксона може бути вдосконалений по декількох напрямах:

 можна замінити процедуру генерації  -чисел так, щоб вірогідність їх породження була більшою;

 можна оптимізувати вибір бази, чинника, з тим, щоб зменшити число невідомих в системі рівнянь;

 можна удосконалити процедуру відсіву „поганих” чисел , що не є -числами;

 можна використовувати швидкий алгоритм рішення системи лінійних рівнянь ( наприклад, алгоритм Відемана для розріджених матриць), і т.д.

 Подібні поліпшення не дозволяють змінити загальний вид оцінки складності    але дають можливість зменшити константу ,

 Алгоритм  Брілхарта - Моррісона.

 Суть алгоритму Брілхарта - Моррісона, опублікованого ними в 1975 р., полягає в двох змінах в алгоритмі Діксона:

 випадкові числа  вибираються за допомогою методу безперервних дробів, запропонованого Лагранжем, що дозволяє генерувати такі , що  є малим, і тому вірогідність його розкладання вища;

           з фактор-бази   виключаються ті числа , для яких

 

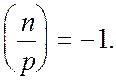
 Розглянемо алгоритм детальніше.

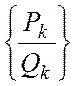 Теорема. Хай   - дійсне число, і  - послідовність його підходячих дробів ,  Тоді при всіх   виконується нерівність

 

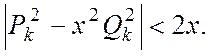
 Доказ. Через властивості відповідних дробів маємо

 

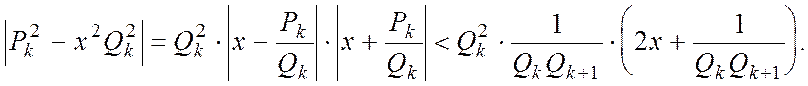
 Звідси

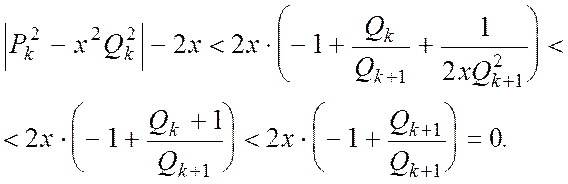
 Слідство. Хай   не є квадратом і   - відповідний дріб для числа . Тоді мінімальний по абсолютній величині лишок

 рівний   і не перевершує

 Доказ.  При

 ,

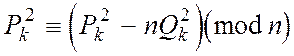 причому через теорему 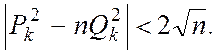 Тому мінімальний по абсолютній величині лишок числа   по модулю  співпадає з , що і потрібно було довести.

 Дана властивість показує, що якщо як випадкові числа   на 1 етапі алгоритму Діксону брати числа ,  то мінімальний по абсолютній величині лишок числа , рівний , не перевищуватиме значення .. Тому вірогідність його розкладання в добуток чисел бази  буде вищою, ніж при випадковому виборі.

 Метод квадратичного решета.

 У 1981 році К. Померанц запропонував для породження - чисел використовувати підхід, узагальнюючий метод Ферма.

 Розглянемо функцію

 ,

 що є квадратним тричленом з цілими коефіцієнтами.

 При кожному цілому   виходить нетривіальне порівняння

 ,

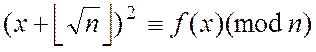 причому значення   при малих   невелике:

 

 і тому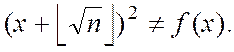

 Тому, якщо замість випадкових чисел в алгоритмі розглядати значення   при випадкових , що знаходяться в деякому інтервалі , то вірогідність породження - чисел зростає.

 При цьому можна заздалегідь здійснити просіювання тих   з цього інтервалу, які можуть давати розкладання   на множники з фактор-бази   Для цього для кожного , яке може виступати як співмножник в розкладанні

 

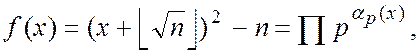
 вирішуємо квадратне рівняння

 

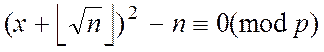
 у кільці . Якщо  - рішення цього рівняння, то повинна виконуватися рівність

 Виконавши заздалегідь дану роботу по знаходженню коріня  для кожного , можна тепер залишити в інтервалі   тільки ті числа,  для яких порівняння  виконується для достатньо великої кількості чисел . Знання для кожного  списку тих, для яких виконуються ці порівняння, допоможе також швидше здійснити факторизацію числа   якщо вона існує.

 Дж. Девіс і П. Монтгомері узагальнили даний підхід. Вони запропонували використовувати многочлен

 

 де коефіцієнти  є цілими числами і удовлерворяют умові

;

 При такому виборі коефіцієнтів виконується рівність

 звідки одержуємо порівняння

 причому

 Коефіцієнти  вибираються, виходячи з таких міркувань. Функція   приймає максимальне значення в кінцях відрізка

 Мінімальне значення вона приймає в крапці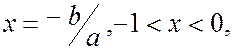

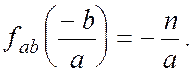
 Вибиратимемо     так, щоб максимальне і мінімальне значення функції   на відрізку  були рівні по абсолютному значенню і протилежні по знаку:

 

                                                   f(x)

 

                      -М                

 

                                                                                 М                       x

 Тому вважаємо:

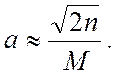
 Число  знаходимо як рішення порівняння

 Нарешті число  вибираємо з умови

 Помітимо, що умову існування рішення другого порівняння можна перетворити таким чином: для всіх простих дільників  виконується 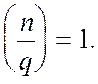  Значення факторизації числа   необхідно також тому, що воно бере участь як співмножник в шуканому порівнянні. Тому, звичайно, як число  вибирають або повний квадрат, або число, що факторизується в добуток простих чисел з фактор-бази.

 При даному виборі параметрів значення многочлена  на інтервалі

  задовольняє нерівності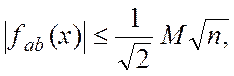

 що в   разів краще, ніж у початкового алгоритму Помаранчі, в якому при  

 Завдання.

 Методом Ферма і Діксону факторизувати числа, вказані в таблиці 1. Оцінити складність обчислень. Варіант брати залежно від номера в журналі.

Варіант (номер в журналі)	1	2	3	4	5	6	7	8	9	10	11	12
Число (факторизувати методом Ферма)	143	187	221	247	253	347	323	437	391	77	249	377
Число(факторизувати методом Діксона)	437	323	347	253	247	221	187	143	77	527	403	203

Варіант (номер в журналі)	13	14	15	16	17	18	19	20	21	22	23	24
Число (факторизувати методом Ферма)	203	341	403	527	203	217	377	391	221	347	249	247
Число (факторизувати методом Діксона)	341	403	249	377	143	203	217	77	527	187	323	341

Таблиця 1.