Практичне заняття №1 (ТСО).
Ціль заняття: Ознайомитися з простими арифметичними алгоритмами і методами оцінки їх складності.
Прості алгоритми і їх складність.
Складання і віднімання.
Помітимо, що стандартні шкільні алгоритми складання і віднімання чисел стовпчиком, мають оцінку складності O(log N), де N- більше з двох чисел. Це мінімально можлива оцінка складності. Ми розглядаємо оцінку складності з точністю до константного множника.
Множення і ділення.
Для множення і ділення двох чисел N і M алгоритми множення стовпчиком і ділення кутом дають оцінку O(log N log M) . Тому для функцій оцінки складності множення і ділення двох n- розрядних чисел виконується нерівність
n£F(n)£O(n2)
Відзначимо, що складнощі операцій множення, ділення із залишком, зведення в квадрат і знаходження зворотного до даного елементу співпадають з точністю до константного множника.
Позначимо M(n) - складність операції множення двох n-розрядних чисел, D(n) - складність операції ділення із залишком 2n- розрядного числа на n- розрядне число, S(n)- складність операції зведення в квадрат n -розрядного числа і R(n)- складність операції обернення n- розрядного числа.
Алгоритм Евкліда.
Позначатимемо
НСД чисел А і В через (А, В). Нагадаємо, що алгоритм Евкліда полягає в
послідовному виконанні операції ділення із залишком до отримання нульового
залишку. Хай А > В > 0 . Позначимо A = r-1
, B = r0 і![]() за
за ![]() і
і ![]() . Тоді
. Тоді ![]() і до отримання залишку
і до отримання залишку ![]() необхідно
виконати
необхідно
виконати ![]() ділення.
ділення.
Оцінка складності алгоритма Евкліда
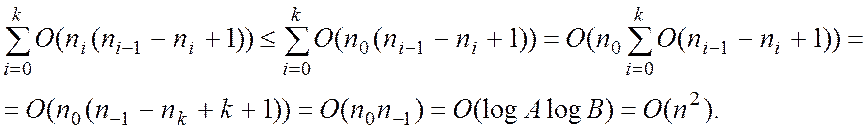
Розширений алглритм Евкліда.
Розглянемо тепер розширений
алгоритм Евкліда, що дозволяє разом з найбільшим загальним дільником чисел ![]() і
і ![]() знаходити
цілі числа
знаходити
цілі числа ![]() і
і ![]() , що
задовольняють рівності
, що
задовольняють рівності ![]() . Від
звичайного алгоритму Евкліда він відрізняється тим, що разом з послідовністю
залишків
. Від
звичайного алгоритму Евкліда він відрізняється тим, що разом з послідовністю
залишків ![]() обчислюються ще дві допоміжні
послідовності
обчислюються ще дві допоміжні
послідовності ![]() і
і ![]()
Наприклад
5x +7y НСД (5,7 )
1. r- 1 = 5; r0 = 7
x - 1 = 1; y - 1 = 0; x 0 = 0; y 0 = 1
d 1 = ë r - 1 / r 0 û = ë 5 / 7 û = 0
r 1 = r - 1 - d 1 r 0 = 5 - 0´ 7 = 5
x 1 = x - 1 - d1 x 0 = 1 - 0´ 0 = 1
y 1 = y - 1 - d 1 y 0 = 0 - 0´ 1= 0
2. d 2 = ë r 0 / r 1 û = ë 7 / 5 û = 1
r 2 = r 0 - d 2 r 1 = 7 - 1´ 5 = 2
x 2 = x 0 - d2 x 1 = 0 - 1´ 1 = - 1
y 2 = y 0 - d 2 x 1 = 1 - 1´ 0= 1
3. d 3 = ë r 1 / r 2 û = ë 5 / 2 û = 2
r 3 = r 1 - d 3 r 2 = 5 - 2´ 2 = 1
x 3 = x 1 - d3 x 2 = 1 - 2´ ( - 1) = 3
y 3 = y 1 - d3 y 2 = 0 - 2´ 1= - 2
4. d4 = ër2 / r3 û = ë 2 / 1 û = 2
r4 = r2 - d 4 r3= 2 - 2´ 1 = 0
Справді знайдені числа ![]() і
і ![]() , що задовольняють рівності
, що задовольняють рівності
![]() Д(5,7)
Д(5,7)
5 ´ 3 +7´ ( - 2 ) = НОД (5,7 )
Сам алгоритм можна представити таким чином:
r- 1 = А; r0 = B
x - 1 = 1; y - 1 = 0; x 0 = 0; y 0 = 1
for i = 1 until r i > 0 do
begin
d i = ë r i - 2 / r i - 1 û ;
r i = r i - 2 - d i r i - 1 ;
x i = x i - 2 - d i x i - 1 ;
y i = y i - 2 - d i y i - 1 ;
i = i + 1;
end
Значення ![]() і
і
![]() при яких
при яких ![]() будуть
шуканими.
будуть
шуканими.
Складність цього алгоритму відрізняється від складності звичайного алгоритму Евкліда не більше, ніж на константний співмножник, і складає
![]() ,
де
,
де ![]() довжина
запису чисел
довжина
запису чисел ![]() і
і![]()
Складання, віднімання.
При складанні чисел в інтервалі ![]() . Сума
. Сума ![]() може вийти за межі
інтервалу, тому може знадобитися ще одне віднімання
може вийти за межі
інтервалу, тому може знадобитися ще одне віднімання ![]() . ( 13 (mod 17) + 8 (mod 17) = 13 + 8
-17 =
4 (mod 17 )) Аналогічно, при відніманні може потрібно ще одне складання
. ( 13 (mod 17) + 8 (mod 17) = 13 + 8
-17 =
4 (mod 17 )) Аналогічно, при відніманні може потрібно ще одне складання ![]() . (7 (mod 13) - 12 (mod 13)
= 7 - 12 +
13 = 8 (mod 13 )) Тому, складність цих операцій рівна
. (7 (mod 13) - 12 (mod 13)
= 7 - 12 +
13 = 8 (mod 13 )) Тому, складність цих операцій рівна ![]() .
.
Множення.
Для знаходження лишку, відповідного добутку
двох лишків, треба виконати одне множення ![]() -розрядних чисел і одне ділення
-розрядних чисел і одне ділення ![]() -розрядного
числа на
-розрядного
числа на ![]() -розрядне.
Тому, складність даної операції рівна
-розрядне.
Тому, складність даної операції рівна ![]() .
.
У багатьох випадках, особливо при
апаратній реалізації алгоритмів, зручно відмовитися від операцій множення і
ділення і замінити їх операціями складання.
Один з таких алгоритмів, що був запропонований П.Л.
Монтгомері в 1985 році., полягає в наступному. Хай ![]() -непарне
число, потрібно помножити лишки
-непарне
число, потрібно помножити лишки 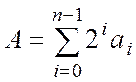 і
і ![]() . Розглянемо
алгоритм:
. Розглянемо
алгоритм:
R = 0;
for i = 0 until i < n do
begin
if ai = 1 then R = R + B;
if R - непарне then R = R + N;
R = R / 2;
end
if R ³ N then R = R - N.
Сутність даного алгоритма в тому, що в силу рівності
A = 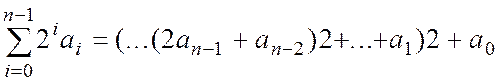
множення числа В на число А зводиться до обчислення виразу
AB = ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.