Знайомство з простими арифметичними алгоритмами і методами оцінки їх складності (Практичне заняття № 1), страница 2

Воно виконується за  кроків,  на кожному з яких здійснюється додавання до поточного значення  значення ,  з подальшим діленням на 2. Завдяки цьому діленню отримані значення завжди знаходяться в інтервалі .  В результаті роботи даного алгоритму виходить число . Тепер для отримання числа  необхідно застосувати ще один раз даний алгоритм до чисел  і . Оскільки число  обчислюється за допомогою зсувів і віднімань з складністю  двійкових операцій (його можна обчислити наперед і зберігати отримане значення), а алгоритм також виконується за  операцій, то загальна трудомісткість обчислення добутку оцінюється величиною   двійкових операцій.

 Наприклад:

Нехай А = 1´2⁰ + 0´2¹ + 1´2²  + 0´2³ + 1´2⁴ = 1 + 4 + 16 = 21 (10101)

          В = 18

          N = 41

Зрозуміло, що АВ(mod N) = 21´18(mod 41) = 9

Обчислимо добуток цих чисел за допомогою вищезгаданого алгоритму.

1. R = 0

    a₀ = 1  

    R = R + B = 0 + 18 = 18;

    R - парне;

    R = R / 2 = 9.

2. a₁ = 0;

R - непарне;

R = R + N = 9 + 41 = 50;

R = R / 2 = 25;

3. a₂ = 1

    R = R + B = 25 + 18 = 43;

    R - непарне;

    R = R + N = 43 + 41 = 84;

    R = R / 2 = 42;

4. a₃ = 0;

      R - непарне;

      R = R + N = 1 + 41 = 42;

R = R / 2 = 21;

5. a₄ = 1

    R = R + B = 21 + 18 = 39;

    R - непарне;

    R = R + N = 39 + 41 = 80;

    R = R / 2 = 40.

Це ми одержали 2-n AB(mod N) .Теперь ми повинні ще раз скористатися цим алгоритмом для обчислення АВ (mod N).

A’ = 2²ⁿ (mod N) = 2^{2 ´5}(mod N) = 1024(mod 41) = 40 = 0´2⁰ + 0´2¹ + 0´2²  + 1´2³ + 0´2⁴ + 1´2⁵

B ’= 40;

N = 41.

1. R = 0

    a₀ = 0

    R - парне;

    R = R / 2 = 0.

2. a₁ = 0;

 R - парне;

 R = R / 2 = 0;

3. a₂ = 0

    R - парне;

    R = R / 2 = 0;

4. a₃ = 1;

    R = R + B = 0 + 40 = 40;

    R - парне;

R = R / 2 = 20;

5. a₄ = 0;

    R - парне;

    R = R / 2 = 10;

6.  a₅ = 1;

    R = R + B = 10 + 40 = 50;

    R = R - N = 50 - 41 = 9.

Обернення.

 Для заданого числа , , знаходимоза допомогою розширеного алгоритму Евкліда числа     і  , що задовольняють рівності .  Якщо , то за зворотне можна взяти .

 Таким чином, обернення в кільці лишків можна виконати за  бітових операцій.

 Ділення.

 Оскільки 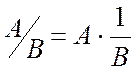, то ділення в кільці лишків виконується з складністю    .

 Індивідуальне завдання.

Завдання 1. За допомогою розширеного алгоритму Евкліда знайти цілі числа і, що задовольняють рівності . Розрахувати складність алгоритму. Дані приведені в таблиці 1.

Варіант (номер засписком )	Рівність
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

Таблиця 1.

Завдання 2. За допомогою алгоритму Монтгомері знайти добуток чисел

 . Оцінити складність алгоритму. Дані узяти з таблиці 2 залежно від номера по журналу.

Варіант (номер засписком )
1	21	18	37
2	19	16	37
3	23	18	37
4	25	16	37
5	25	18	37
6	21	16	41
7	27	20	41
8	25	20	41
9	27	18	41
10	29	16	41
11	21	14	29
12	21	16	29
13	21	12	29
14	19	16	29
15	19	14	29
16	27	18	31
17	27	20	31
18	27	16	31
19	27	14	31
20	25	16	31
21	33	18	47
22	33	16	47
23	35	18	47
24	35	16	47

Таблиця 2.