Криптоперетворення в групі точок еліптичних кривих

Лекція № 7 з дисциплін

„ОСНОВИ ТЕОРІЇ ЗАХИСТУ ІНФОРМАЦІЇ „

ТЕМА ЛЕКЦІЇ

„КРИПТОПЕРЕТВОРЕННЯ В ГРУПІ ТОЧОК ЕЛІПТИЧНИХ КРИВИХ”

Навчальні питання

6.1 Метрики скалярного множення в групі точок  еліптичних кривих.

6.2 Базиси представлення операцій додавання та подвоєння.

6.3 Перетворення в проективних координатах

6.4ДОДАТКИ Основна інформація відносно еліптичних кривих

Джерела що рекомендуються для  самостійної робот

1.  Горбенко І.Д. Основи теорії захисту інформації. Електронний конспект лекцій. Харків, ХНУРЕ, 2005 р.

2.  Горбенко І.Д. „Криптографічний захист інформації”. Навч. посібник Харків, ХНУРЕ, 2004 р.

3.В. Задірака . Компьютерная криптологія. Підручник. К, 2002 ,504с.

            4.А.Бессалов,А.Телиженко. Криптосистемы 

                  эллиптических        кривых. Киев, «Политехника», 2004 г. 223 с.

 Додаткова література

1.  А. Менезис, П. Ван Аршот, С. Ватсон. Руководство по прикладной криптографии CRC Press, 1997, электронная копия, 662 с

2.Брюс Шнайер. Прикладная криптография. М., изд. Триумф. 2002 г., 797 с

6.1 Метрики скалярного множення в групі точок  еліптичних кривих.

При криптографічних перетвореннях в групі точок еліптичних кривих основною операцією є скалярне множення. Наприклад,  операція  обчислення відкритого ключа є у наступному:

,                                                         (6.1)

де  – особистий ключ, як правило випадкове число:

, де  – порядок базової точки ;

 – модуль перетворення над полем Галуа F(q):

;

 – відкритий ключ, що задається на площині ( є  точкою на еліптичній кривій):

.

 – еліптична крива над простим полем, задається рівнянням:

,                                           (6.2)

де  – параметри еліптичної кривої.

                                                      (6.3)

Точка  еліптичній кривій (6.2), якщо при підстановці їх значень в порівняння еліптичної кривої ліва частина не порівнюється з правою за .

В афінному  базисі (6.1) можна представити:

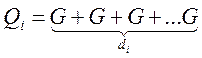                                            (6.4)

При виконанні (6.4) виділяють 2 операції: операція подвоєння – складаються 2 однакові точки, і операція додавання – складаються 2 різні точки

                                                   та            (6.5)

Сума цих точок на ЕК:

                                           (6.6)

При подвоєнні 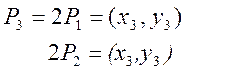                           або              (6.7)

Можна показати що операція складання  на ЕК над полем GF(P)

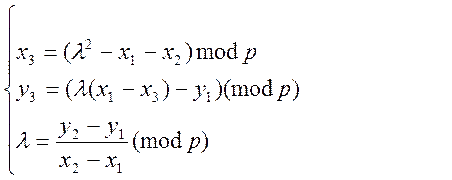                                                                                                                  (6.8)

Таким чином (6.8) – визначає метрику додавання 2 точок.

Для випадку  подвоєння точки

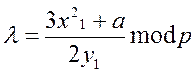                                                                              (6.9)

Геометрична інтерпретація складання двох точок наведено на рис .1.

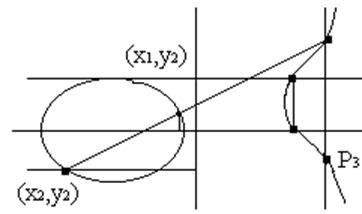                                                                     Рисунок 1.5.1

Над розширенням поля  рівняння еліптичної кривої має вид:

                                                (6.10)

 – точка на ЕК,

 – коефіцієнти (параметри) ЕК

f(x) – примітивний поліном над полем .

                                                                                                              (6.11)

Поліном називається примітивним, якщо він що не приводиться, а з іншої сторони породжує поле порядку .

Для поля  координати точки   при подвоєнні визначаються як:

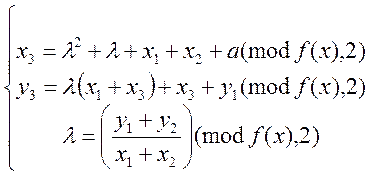                                   (6.12)

Точка, що подвоєна, має координати:

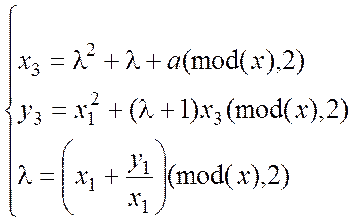.                              (6.13)

У (6.12) та (6.13) усі параметри є поліномами не вище m-го ступеня, а F(x) – примітивний поліном над .

6.2 Базиси представлення операцій додавання та подвоєння

В групах точок еліптичних кривих існує три базиси представлення:

1) афінний;

2) проективний;

3) змішаний.

Афінний базис

Для поля ,

                                                (6.14)

де  - точки ЕК    

 – параметри ЕК,  

У порівнянні (6.14) , а також а, b – коефіцієнти, є поліномами не вище m – порядку

m³160        .

Афінний базис вимагає великої обчислювальної складності.

                                             (6.15)

  - базова точка.

d – особистий секрет ключа     

n – порядок (період) базової точки G.

Для зменшення чи складності підвищення швидкості використовується проективний базис. Проективний базис є трьохмірним, тобто кожна точка задається трьохмірно:

                (X,Y,Z)

при цьому перехід з афінного представлення в проективний:

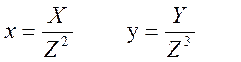                                                                     (6.16)

підставимо (6.16) у (6.14).

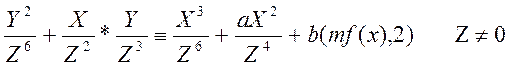
                                            (6.17)

(6.17) задає ЕК над полем  у проективному базисі.

6.3 Перетворення в проективних координатах

Рівняння кривої в проективних координатах має вигляд

.                   (6.17)

Можна показати, що операції додавання і подвоєння для кривої можуть бути обчислені у такому вигляді [14]:

,   ,   .

,      ,              ,                       (6.18)

,     ,              ,

,          ,            ,

.

При обчисленні подвоєної точки в проективних координатах

, , ,

, ,                           (6.19)

.

Основною особливістю використання проективних координат є те, що в цьому базисі не виконується операція ділення за модулем, яка зводиться до знаходження зворотного елемента. Так в афінному базисі необхідно для різних кривих та операцій знаходити значення: