Криптоперетворення в групі точок еліптичних кривих, страница 4

Зворотній елемент групи

Нехай  буде елементом групи . Тоді для кожного елемента  існує однозначний елемент  такий, що . Елемент  називається мультиплікативно зворотнім до елемента , позначається як , та може бути обчислений як .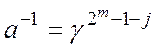

Характеристика скінченного поля

Якщо при обчисленні  для одержання  необхідно  додавань, то  називається характеристикою поля. Якщо нульовий елемент шляхом зазначеного додавання не може бути одержано, тоді  є нулем, а не нескінченним елементом .

Ділення у полі

Значення частки  в полі  існує, якщо знаменник не нульовий. У цьому випадку частка обчислюється як , тобто множенням елемента  на зворотний .

Скінченні поля, які використовуються у цьому параграфі, розглядаються у вигляді упорядкованого набору елементів. Це дозволяє здійснювати перетворення послідовно.

А.2.2 Еліптичні криві над полем

У цій частині наведено два різних, але еквівалентних описи еліптичних кривих, що визначені над скінченними простими полями характеристики двійки.

А.2.2.1 Афінне подання

Нехай  для деяких цілих  є скінченним полем. Еліптична крива  над цим полем задається рівнянням вигляду:

,                                                 (А.2.1)

причому  та .

Еліптична крива  над полем , що визначається рівнянням типу (А.2.1), складається з набору точок , для яких виконується рівняння . Цій еліптичній кривій також належить додаткова точка , що називається точкою нескінченності кривої .

Точка нескінченності  не належить до  і не задовольняє рівнянню (А.2.1). Набір точок кривої  типу  називається афінним поданням кривої .

А.2.2.1.1 Груповий закон в афінному поданні

Для еліптичної кривої  над полем  задано бінарну операцію :, яка дозволяє для двох точок  кривої  обчислити третю точку , що належить кривій . Еліптична крива  є абелевою групою відносно операції  і має такі властивості:

-  точка нескінченності  для групової операції на кривій  є нейтральним елементом, тобто , для всіх точок  кривої ;

-  якщо точка є афінним поданням на кривій , тоді інверсна точка  має координати  та ;

-  якщо точки  та  є афінними точками кривої , причому , тоді координати  суми  визначаються такими формулами:

;                                                 

;                                       (А.2.2)

,                                                     

якщо ;

або

;                                                       

;                                    (А.2.3)

,                                                     

якщо .

Таким чином формули додавання та подвоєння точок еліптичної кривої  є різними.

При використанні додавання та подвоєння в полі  згідно з (А.2.2) та (А.2.3) найбільш складною при афінному поданні є операція ділення за модулем. При проективному поданні виконання операцій додавання та подвоєння здійснюється без операції ділення за модулем. Афінне та проективне подання точок є сумісними.

А.2.2.2 Проективне подання

Проективне подання еліптичних кривих визначених над скінченним полем  наводиться нижче.

При використанні проективного подання точок еліптичної кривої  операція ділення за модулем при додаванні та подвоєнні точок не виконується, але збільшується число множень над полем.

А.2.2.2.1 Проективні площини над полем

Розглянемо набір точок , що складається із усіх трійок  елементів поля , крім трійки . Введемо в множину  відношення еквівалентності, яке позначимо символом “~”. Це відношення еквівалентності має такі властивості: , якщо існує  таке, що  та .

Проективна площина  над полем  є набором еквівалентних класів, які визначаються операцією . Еквівалентний клас, якому належить трійка  визначається як .  Цей еквівалентний клас називається точкою проективних координат над полем . При цьому точка  не належить площині .

А.2.2.2.2 Проективне подання еліптичної кривої  над полем

Проективним аналогом афінному рівнянню Вейєрштрасса (А.2.1) є гомогенне кубічне рівняння

,                            (А.2.4)

у якому

Еліптичні криві в проективному поданні складаються із всіх точок  проективної площини , таких, що кожна трійка  є розв’язком рівняння (А.2.4). Між точками  та  афінного та проективного подань  існують однозначні відображення, це досягається виконанням таких умов:

-  якщо  є афінною точкою на кривій , тоді  є відповідною точкою в проективному поданні;