Криптоперетворення в групі точок еліптичних кривих, страница 5

-  якщо  з  є розв’язанням (А.2.4), тоді  є відповідною афінною точкою на кривій ;

-  існує тільки одне розв’язання (А.2.4) з , а саме точка . Ця точка відповідає точці нескінченності .

А.2.2.2.3 Груповий закон проективного подання

При проективному поданні кривої (А.2.4) точки кривої мають такі властивості:

-  точка  є нейтральним елементом  відносно ;

-  нехай  буде проективним поданням точки на кривій , тоді  є точкою ;

-  нехай  та  будуть двома різними точками на кривій , причому обидві не рівні , тоді їх сума позначається як . Координати   та  точки  обчислюються з використанням формул:

;                                                        

;                             (А.2.5)

,                                                   

де , , та ;

-  якщо , то координати точки подвоєння ,  обчислюються з використанням формул:

;                                                         

;                              (А.2.5)

,                                                         

де  та .

А.3 Скінченне поле

А.3.1 Визначення поля

Як зазначено в розділі 5, для будь-яких простих  і позитивного цілого числа  існує скінченне поле, що складається точно з  елементів.  Це поле однозначно визначене з точністю до ізоморфізму та у цьому документі подане як скінченне поле .

Для елементів поля  введено дві основні операції – додавання за модулем  та множення за модулем , причому:

-     є абелевою групою, у відношенні до операції додавання за модулем ;

-   є абелевою групою, у відношенні до операції множення за модулем .

Існує багато способів побудови скінченного поля з  елементів. Скінченне поле  може бути відображене як векторний простір розмірності  над полем . Тобто, існує  елементів  у полі  таких, що кожний елемент  може бути однозначно поданий у формі , де . Такий, набір  елементів називається базисом поля  над полем . При використанні такого базису елемент поля  може бути наведений у вигляді вектора . Такий елемент поля позначається -арним рядком  довжини , тобто .

Існує багато різних базисів  над полем . Відповідно для кожного базису можуть бути визначені розмір множини елементів поля та операція множення.

Множина  позначається як . Вона має порядок . Причому, існує в крайньому випадку хоча б один елемент  у групі  такий, що кожний елемент  у мультиплікативній групі  може бути однозначно записаний як , де .

Зворотній елемент групи

Нехай  буде елементом групи . Тоді для нього однозначно існує елемент  такий, що . Елемент поля  називається мультиплікативно зворотним до елементу . Він позначається як , та може бути обчислений як .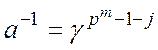

Характеристика скінченного поля

Якщо при обчисленні  для одержання  необхідно  додавань, то  називається характеристикою поля. Якщо нульовий елемент шляхом вказаного додавання не може бути одержано, тоді  є нулем, а не нескінченним елементом .

Ділення у полі

Частка  в полі  існує, якщо знаменник не є нульовим. За даної умови частка обчислюється множенням в полі  на зворотний елемент , тобто .

Квадрати й не квадрати в полі

Припустимо, що . Елемент  називається квадратом у полі , якщо існує елемент  такий, що . Факт існування квадратного кореня визначається за умовою:

       є квадратом у полі , якщо .

Пошук квадратного кореня в полі

Для знаходження квадратних коренів у полі  існують різні методи. Їх застосування дозволяє для кожного  знайти  таке, що . Приклади таких методів наведені в [1] та [3].

Примітка. Скінченні поля, які використовуються у цьому параграфі, розглядаються у вигляді упорядкованого набору елементів. Це дозволяє здійснювати перетворення послідовно.

А.3.2 Еліптичні криві над полем

У цій частині вводиться два різних, але еквівалентні подання еліптичних кривих, визначених над скінченними полями.

А.3.2.1 Афіне подання

Нехай  буде скінченним простим полем, причому . Еліптична крива  над полем  визначається несингулярним кубічним рівнянням над полем . У цьому стандарті припускається, що  крива  задається рівнянням Вейєрштрасса вигляду

,                                         (А.3.1)

причому  та виконується умова  у полі . Рівняння (А.3.1) називається аффіним рівнянням Вейєрштрасса.

Еліптична крива  над полем , визначена рівнянням вигляду (А.3.1), складається з набору таких точок , для яких справедливим є рівняння 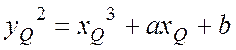, в тому числі і для додаткової точки , що називається точкою нескінченності кривої .