



Министерство Образования Российской Федерации
Новосибирский Государственный Технический Университет
Зачетная работа
По дисциплине: Общая алгебра
Вариант №186
Группа ПМ-22
Студент: Савлюк В.И.
Преподаватель: Пинус А.Г.
г.Новосибирск
2004
Задание 1.
Будет ли функция f условно-термальной (программно-вычислимой) на алгебре
![]() , где
, где
|
X |
Y |
F(x,y) |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
0 |
2 |
2 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
|
1 |
2 |
1 |
|
2 |
0 |
2 |
|
2 |
1 |
0 |
|
2 |
2 |
2 |
|
y\x |
0 |
1 |
2 |
|
0 |
0 |
2 |
0 |
|
1 |
1 |
1 |
0 |
|
2 |
1 |
2 |
2 |
Для проверки условия программной вычислимости сначала найдем все подалгебры и проверим замкнутость функции f(x,y) на них.
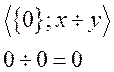
Подалгебра. Проверим замкнутость: ![]() –
замкнута.
–
замкнута.
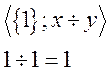
Подалгебра. Проверим замкнутость: ![]() –
замкнута.
–
замкнута.
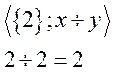
Подалгебра. Проверим замкнутость: ![]() –
замкнута.
–
замкнута.
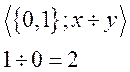
Не подалгебра.
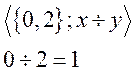
Не подалгебра.
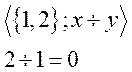
Не подалгебра.
![]() – сама алгебра А. Тоже
подалгебра.
– сама алгебра А. Тоже
подалгебра.
Функция f(x,y) – замкнута относительно этой подалгебры.
Теперь проверим, чтобы наша функция коммутировала со всеми изоморфизмами среди подалгебр алгебры А.
Проверяем на внешние изоморфизмы между подалгебрами:
![]()
Изоморфизм ![]()
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
Функция удовлетворяет условиям этого изоморфизма. Очевидно,
что она удовлетворяет и условиям изоморфизма ![]()
Изоморфизм ![]()
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
2 |
2 |
2 |
2 |
0 |
2 |
2 |
Функция удовлетворяет условиям этого изоморфизма и
изоморфизма ![]()
Изоморфизм ![]()
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
2 |
2 |
2 |
2 |
1 |
2 |
2 |
Функция удовлетворяет условиям этого изоморфизма и
изоморфизма ![]()
Теперь рассмотрим все внутренние изоморфизмы в подалгебре ![]() .
.
Рассмотрим изоморфизм:
![]()
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
|
0 |
2 |
1 |
2 |
1 |
0 |
2 |
2 |
0 |
|
|
1 |
0 |
2 |
0 |
2 |
1 |
0 |
1 |
2 |
|
|
1 |
1 |
1 |
2 |
2 |
2 |
2 |
1 |
2 |
|
|
1 |
2 |
2 |
0 |
2 |
0 |
0 |
1 |
2 |
|
|
2 |
0 |
0 |
1 |
0 |
1 |
1 |
2 |
0 |
|
|
2 |
1 |
0 |
1 |
0 |
2 |
1 |
0 |
1 |
|
|
2 |
2 |
2 |
0 |
0 |
0 |
0 |
2 |
0 |
Так как на данном изоморфизме в подалгебре функция не удовлетворяет поставленным условиям – функция не является условно-термальной.
Задание 2.
Укажите все подгруппы групп Sym{1,2}, Sym{1,2,3}
Sym A – симметрическая группа
множества А, определяемая, как ![]() –группа всех биекций
множества А самого на себя. Где
–группа всех биекций
множества А самого на себя. Где ![]() –совокупность всех
взаимно-однозначных отображений множества А на себя,
–совокупность всех
взаимно-однозначных отображений множества А на себя, ![]() –
обратное отображение к отображению
–
обратное отображение к отображению ![]() из
из ![]() . Таким образом, для х, у из А:
. Таким образом, для х, у из А: ![]() . Через
. Через ![]() –тождественное
отображение.
–тождественное
отображение.
Подгруппа – подалгебра произвольной группы.
Рассмотрим группу ![]() .
.
Определим для нее ![]() Других
взаимно-однозначных отображений на себя множество А не имеет. Соответственно,
рассмотрим, будут ли являться подалгебрами:
Других
взаимно-однозначных отображений на себя множество А не имеет. Соответственно,
рассмотрим, будут ли являться подалгебрами:
1. ![]()
![]()
![]() ,
т.к. обратное отображение к
,
т.к. обратное отображение к ![]() , есть
, есть ![]()
Операция ![]() замкнута
относительно
замкнута
относительно ![]() , т.к.
, т.к.
![]() (по свойству групп)
(по свойству групп)
Значит ![]() –
подалгебра, следовательно, является подгруппой.
–
подалгебра, следовательно, является подгруппой.
2. ![]()
![]() . Очевидно, что это тождественное
отображение и обратное к нему является им самим.
. Очевидно, что это тождественное
отображение и обратное к нему является им самим.
Рассмотрим теперь группу Sym{1,2,3}
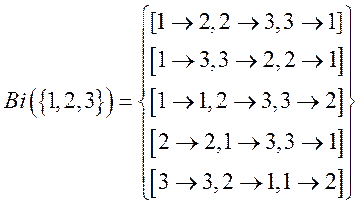
Рассмотрим все подалгебры:
1. ![]()
![]() – не подалгебра
– не подалгебра
2. ![]()
![]() – не подалгебра
– не подалгебра
3. ![]()
Подалгебра, т.к. ![]()
4. ![]()
Подалгебра, т.к. ![]()
5. ![]()
Подалгебра, т.к. ![]()
6. ![]()
Подалгебра.
Теперь, аналогично рассмотренным множествам мощности 1,
выберем множества мощности 2, которые будут являться подалгебрами. Для этого на
![]() определим операцию
определим операцию ![]() ,
как обычную суперпозицию отображений.
,
как обычную суперпозицию отображений.
7. 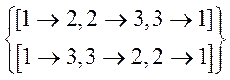 – подалгебра
– подалгебра
8. 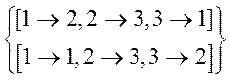 – не подалгебра, т.к.
– не подалгебра, т.к. ![]() , а отображения
, а отображения ![]() нет
нет
9. 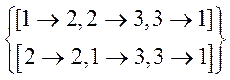 –не подалгебра
–не подалгебра
10. 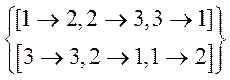 –не подалгебра
–не подалгебра
Остальные подмножества подалгебрами являться не будут, кроме всего множества Bi(A)
Ответ: Bi (A),
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
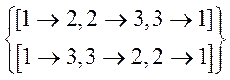 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.