

1. Найти область определения функции и значения (возможно бесконечные) этой функции в точках разрыва и граничных точках области определения.
2. Установить,
является ли функция четной, нечетной, периодической. При наличии симметрии или
периодичности выбрать подобласть области определения для дальнейшего исследования
(п.3-6 выполнять для выбранной подобласти).
3. Найти асимптоты графика (вертикальные – в точках разрыва и граничных точках области определения; наклонные или горизонтальные – если функция определена на полупрямой или на всей числовой прямой).
4. Найти нули
функции, т.е. решить уравнение ![]() .
.
5. Вычислить первую производную функции. Найти локальные экстремумы функции и промежутки ее возрастания и убывания.
6. Вычислить вторую производную. Найти промежутки сохранения направления выпуклости.
7. Определить характер особых точек кривой.
8. Построить таблицу (см. ниже).
9. Построить график функции. Если в п.2 была установлена симметрия или периодичность, то дорисовать функцию на всю область определения соответствующим образом.
x = x(t), y = y(t), tÎT
1. Найти общую часть областей определения функций x(t), y(t).
2. Установить, обладает ли кривая симметрией (если кривая обладает симметрией, то можно сократить выкладки, ограничив соответствующим образом исследуемую часть области определения).
4Четыре основных случая симметрии:
![]()
![]() ,
, ![]() – симметрия относительно оси
– симметрия относительно оси ![]() .
.
![]()
![]() ,
, ![]() – симметрия относительно оси
– симметрия относительно оси ![]() .
.
![]()
![]() ,
, ![]() – симметрия относительно точки
– симметрия относительно точки ![]() .
.
![]()
![]() ,
, ![]() – наложение ветвей графика. 3
– наложение ветвей графика. 3
3. Определить, не обладает ли данная кривая периодичностью на исследуемой части области определения.
4Условия периодичности:
Из того, что y(t) периодична, а x(t) – функция с неограниченной областью значений и периодичной производной, следует периодичность y(x), а из того, что x(t) периодична, а y(t) – функция с неограниченной областью определения и периодичной производной, следует периодичность x(y). 3
4. Найти асимптот графика функции y(x).
4Условия существования асимптот:
Если при ![]()
![]() , а
, а ![]() , то
, то ![]() – вертикальная
асимптота кривой.
– вертикальная
асимптота кривой.
Если при ![]()
![]() , а
, а ![]() , то
, то ![]() –
горизонтальная асимптота кривой.
–
горизонтальная асимптота кривой.
Если при ![]()
![]() и
и ![]() , то возможна наклонная асимптота
, то возможна наклонная асимптота ![]() , где
, где 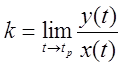 ,
, ![]() ,
, ![]() .
.
Отметим, что символ S может
принимать следующие значения: ![]() ,
, ![]() , где
, где ![]() ,
, ![]() ,
, ![]() . 3
. 3
5. Найти нули функций x(t), y(t) и их области знакопостоянства.
6. Найти точки tk, в которых хотя бы одна из производных x′(t), y′(t) равна нулю или разрывна.
4Точки ti,
найденные в пункте 4, и точки tk,
найденные в этом пункте, разбивают множество T
на промежутки знакопостоянства производных x′(t), y′(t), и, следовательно, данная система уравнений на
интервале (tp, tp+1)
задаёт параметрическую функцию вида ![]() ,
которая является одной из веток исходной кривой. 3
,
которая является одной из веток исходной кривой. 3
7. Найти
вторую производную данной параметрической функции 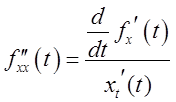 , где
, где 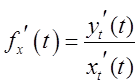 , и те точки tj,
в которых
, и те точки tj,
в которых ![]() .
.
8. Определить направление выпуклости каждой ветви графика функции.
4Если на интервале существует вторая производная функции и если эта производная положительна (отрицательна), то график этой функции на данном интервале имеет выпуклость, направленную вниз (вверх). 3
9. Определить точки экстремума функции (вершины кривой).
4Для этого предварительно выделить точки возможного экстремума, то есть такие точки x(tp), где tp – одно из значений, найденных в пунктах 4,6 и 7 такое, что x′(t) сохраняет знак на интервале (tp-1, tp+1). Затем, рассмотрев изменение y на интервалах (tp-1, tp) и (tp, tp+1), выяснить, является ли x(tp) точкой экстремума. 3
10. Определить характер особых точек кривой.
11. Составить таблицу:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
Интервалы монотонности и точки экстремума |
|||||||||||
|
Интервалы выпуклости и точки |
|||||||||||
|
Особые точки графика и уравнения асимптот |
* Таблица строится только для
тех значений t, для которых определены обе функции –![]() и
и ![]() .
.
** Серым цветом отмечены те клетки таблицы, которые не заполняются;
***Для построения графика
явно заданной функции ![]() используют аналогичную таблицу
(в первой строке – интервалы и значения переменной x, а вторая
строка отсутствует).
используют аналогичную таблицу
(в первой строке – интервалы и значения переменной x, а вторая
строка отсутствует).
12. Пользуясь таблицей и сведениями об особых точках, построить ветви кривой, соответствующие промежуткам (tp, tp+1). Если была установлена симметрия или чётность, то дорисовать функцию на всю область определения соответствующим образом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.