Изгиб балки (расчетно-проектировочное задание)

Федеральное агентство по образованию.

Рыбинская Государственная Авиационно-Технологическая Академия

им. П. А. Соловьева

Кафедра – Теоретическая механика и сопротивление материалов.

Расчетно-проектировочное задание по курсу сопротивление материалов.

Задание № 3

                                                       Вариант №22

Тема: Изгиб балки.

Группа                                                                                   ТИ-03                                                                                

Студент ___________________                                  Синицын И.Н.

                                                                 подпись, дата

Руководитель _______________                                  Бирфельд А.А.                              

                                          подпись, дата

Нормоконтроль _____________

                      Срок сдачи __________

                      Дата сдачи __________

                                               Рыбинск  2004 г.

Задание 3.1.1

Дана балка :

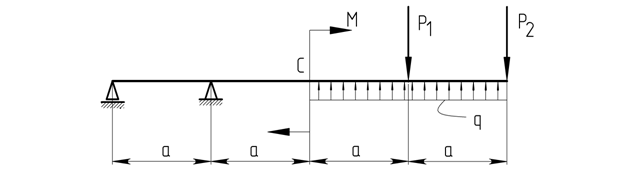
Рисунок 1.1

Форма поперечного сечения : стандартный профиль – двутавр.

Требуется :

1.  записать выражения для поперечных сил и изгибающих моментов на всех участках балки и вычислить их граничные значения;

2.  из условия прочности по нормальным напряжениям рассчитать безопасные размеры балки, т.е. подобрать двутавр. Принять допускаемое напряжение равным 160 МПа;

3.  в сечении, в котором действует максимальная поперечная сила, вычислить величину касательных напряжений на уровне нейтральной оси сечения;

4.  с помощью метода начальных параметров определить углы поворота и прогибы в сечениях балки.

Графическая часть:

1.  построить эпюры поперечных сил и  изгибающих моментов.

2.  вычертить в масштабе поперечное сечение балки

Дано:

         q = 10 ⁴ (Н/м);

            Р₁ = 2·10 ⁴ (Н);

         Р₂ = 0  (Н);

         М = 10 ⁴  (Н·м);

         а = 0,8  (м).

Решение.

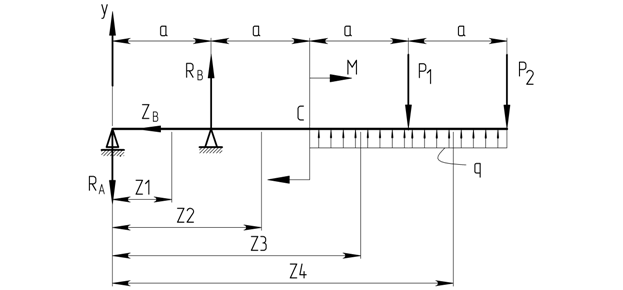
Рисунок 1.2

Определим опорные реакции R_A и R_B :

M_A = 0;

         +R_B ·a – M – P­₁·3a – P₂·4a ­ + q·2a·3a= 0 ;

            +R_B ·0,8 – 10 ⁴ – 2·10 ⁴ ·3·0,8 – 0·4·0,8 ­ +  10 ⁴ ·2·0,8·3·0,8= 0 ;

         R_B = 2,45·10 ⁴.

F_y = 0

         ­–R_A + R_B – P₁ – P₂ + q·2a = 0;

         –R_A + 2,45·10 ⁴ – 2·10 ⁴  – 0 + 10 ⁴ ·2·0,8  = 0

         R_A = ­ 2,05·10⁴  (H).

         Составим выражения поперечных сил и найдем их значения на границах участков:

Q_y1 = ­– R_A ;                      Q_y1 = – 2,05·10⁴ (H);

Q_y2 = ­– R_A + R_B ;             Q_y2 = ­ – 2,05·10⁴  + 2,45·10 ⁴ = 4·10 ³ (H);

Q_y3 = ­– R_A+ R_B­ + q·(z₃ – 2a);  

Q_y3(2a) = – 2,05·10⁴ + 2,45·10 ⁴ = 4·10 ³ (H);