Механика \ Сопротивления материалов

Изгиб балки (расчетно-проектировочное задание), страница 3

+ 104 ·– 2·104 ·  .

Уравнение углов поворота сечений имеет вид:

 E·Ix· θ = E·Ix· у′ = 2,187·10 3– 2,05·104 · + 2,45·104· + 104 · +

 +104 ·– 2·104 ·  .

Давая абсциссе z  различные значения, можно вычислить угловые и линейные перемещения любого сечения балки.

Определим угол поворота и вертикальное перемещение сечения С , находящегося на расстоянии 2·а :

θ(2a) = ·(2,187·10 3– 2,05·104 · + 2,45·104· + +104 ·  +104 ·) = – 8,578·10 –3 (рад);

у(2а) = (2,187·10 3·1,6 – 2,05·104 · + 2,45·104· + +104 ·  + 104 ·) = – 4,447·10 –3  (м).

         Профиль двутавра № 16 представлен на рисунке 1.4  в масштабе  1:2,5:

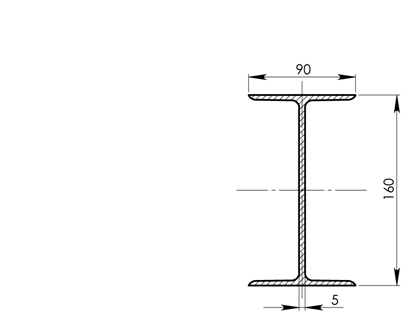
Рисунок 1.4

Задание 3.1.1

Дана балка :

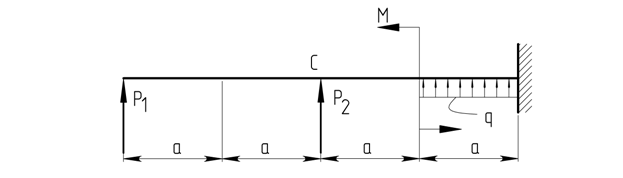
Рисунок 1.5

Форма поперечного сечения : прямоугольник (h = 1,5b).

Требуется :

1.  записать выражения для поперечных сил и изгибающих моментов на всех участках балки и вычислить их граничные значения;

2.  из условия прочности по нормальным напряжениям рассчитать безопасные размеры балки. Принять допускаемое напряжение равным 160 МПа;

3.  в сечении, в котором действует максимальная поперечная сила, вычислить величину касательных напряжений на уровне нейтральной оси сечения;

4.  с помощью метода начальных параметров определить углы поворота и прогибы в сечениях балки.

Графическая часть:

1.  построить эпюры поперечных сил и  изгибающих моментов.

2.  вычертить в масштабе поперечное сечение балки

Дано:

         q = 10 4 (Н/м);

            Р1 = 2·10 4 (Н);

         Р2 = 0  (Н);

         М = 10 4  (Н·м);

         а = 0,8  (м).

Решение.

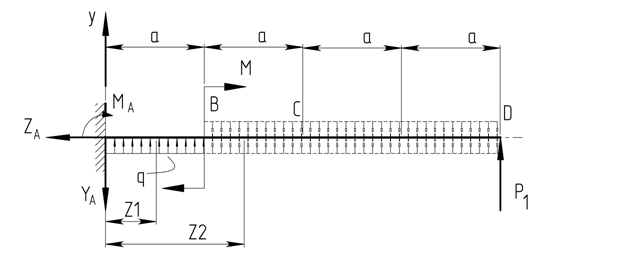
Рисунок 1.6

Определим опорную реакцию YA и момент МА :

MA = 0;

         – MA – M  ­+ q·a·(a/2) + P1 ·4a= 0 ;

            – MA – 104  ­+ 104·0,8·(0,4) + 2·104 ·4·0,8= 0 ;

            MA = 5,72·10 4 (Н·м).

Fy = 0

         ­–YA  – P1  + q·a = 0;

         –­YA  – 2·104  + 104·0,8 = 0;

           YA = ­ 2,8·104  (H).

         Составим выражения поперечных сил и найдем их значения на границах участков:

Qy1 = ­– YA +q·z1;                     Qy1 (0) = – 2,8·104  (H);

                                              Qy1 (a) = – 2,8·104  +104 ·0,8 = –2·104 (H);

Qy2 = ­– YA + q·a ;                    Qy2 = ­ – 2,8·104  +104 ·0,8 = –2·104 (H);

То же для изгибающих моментов:

Mx1 = –YA·z1 +MA + q·z1·z1/2;              

Mx1(0) = MA = 5,72·10 4 (Н·м).

Mx1(a) = –­ 2,8·104  ·0,8 + 5,72·10 4   + 104 ·0,8·0,4= 3,8·104 (H·м);

Скачать файл