Mx2 = – YA·z2 + q·a·(z2 – a/2) + M +MA ;
Mx2(a) = – 2,8·104 · 0,8 + 104 ·0,8·0,4 + 104 +5,72·10 4 = 4,8·104 (H·м);
Mx2(4a) = – 2,8·104 · 4·0,8 +104 ·0,8·2,8 + 104 +5,72·10 4 = 0(H·м);
Эпюры поперечных сил и изгибающих моментов представлены на рисунке 1.7
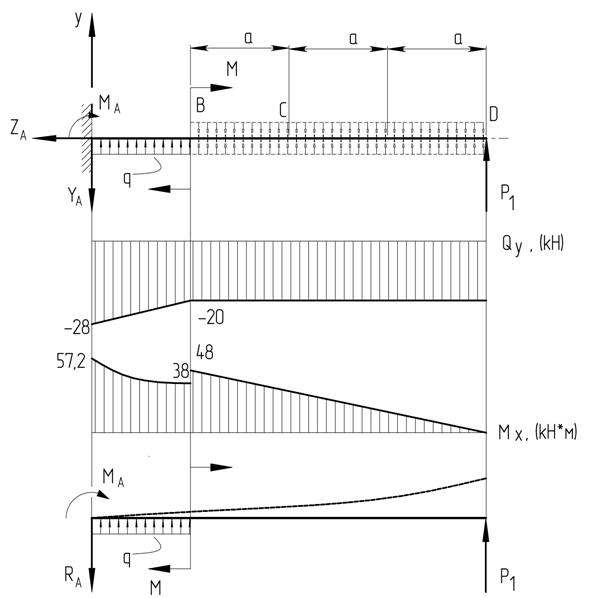
Рисунок 1.7
Условие прочности :
σmax = ≤ [σ] ;
Отсюда : Wx = = = 0,358·10 –3 м3 = 358 (см3);
Wx = = = 358 (см3 );
b=9,85 (см); h=1,5b = 14,78 (см)
Безопасным будет сечение с размерами : b=10 (см), h = 15 (см) и Ix для такой балки будет равен :
Ix = = = 187,5 (см3).
Найдем τmax по формуле:
τmax = ; τmax = = 2,8 (МПа).
Поперечное сечение консольной балки представлено в масштабе 1: 5 на рисунке 1.8 :
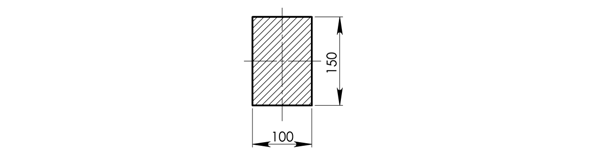Рисунок 1.8
Для составления уравнений перемещений поместим начало координат в левое крайнее сечение балки, распределенную нагрузку q продолжим до конца балки, скомпенсировав ее действие на длине 3·а нагрузкой противоположного направления (рис. 1.6) . Тогда уравнения прогибов (универсальное уравнение ) для данной балки будут иметь вид:
E· Ix · y = E·Ix·y0 + E·Ix· θ 0·z – YA· + MA· + q· │ + M· –– q· │
Здесь последнее слагаемое учитывает распределенную компенсирующую нагрузку. Начальными параметрами являются θ 0 =0 и у0 = 0 (угол поворота сечения и прогиб в начале системы координат, то есть в опоре А).
Перепишем уравнение прогибов с учетом найденных реакций и реактивных моментов, а также с учетом того что θ 0 =0 и у0 = 0 :
E· Ix · y = – 2,8·104· + 5,72·10 4· + 104· │+ 104· – 104 ·│
Уравнение углов поворота сечений имеет вид:
E·Ix· θ = – 2,8·104· + 5,72·10 4· + 104· │+ 104· – 104 ·│
Определим вертикальное перемещение сечения С , находящегося на расстоянии 2·а от левого края балки:
2·1011· 187,5 ·10–6 · y = – 2,8·104· + 5,72·10 4· + 104· + 104· – 104 ·
y = 1,596·10–3 (м).
Определим угол поворота сечения С , находящегося на расстоянии 2·а от левого края балки:
2·1011· 187,5 ·10–6·θ = – 2,8·104· + 5,72·10 4· + 104· + 104· – 104 ·;
θ = 1,857·10 –3 (рад).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.