Механика \ Сопротивления материалов

Изгиб балки (расчетно-проектировочное задание), страница 2

Qy3(3a) = – 2,05·104 +2,45·10 4 + 10 4·0,8 = 1,2·104 (H);

Qy4 = – RA+ RB­ – P1  + q·a+ q·(z4 – 3a);   

Qy4(3a) = – 2,05·104 + 2,45·10 4 – 2·10 4 +104·0,8  = – 0,8·10 4 (H);

Qy4(4a) = – 2,05·104 +2,45·10 4 – 2·10 4 +104·0,8  + 10 4·0,8 = ­0 (H);

         То же для изгибающих моментов:

Mx1 = –RA·z1 ;  

Mx1(0) = 0

         Mx1(a) = –RA·a = – 2,05·104 ·0,8 = –1,64·104 (H·м);

Mx2 = – RA·z2 + RB·(z2 – a) ;

Mx2(a) = – 2,05·104 · 0,8 = –1,64·104 (H·м);

Mx2(2a) = – 2,05·104 · 2·0,8 +2,45·10 4·0,8  = –1,32·104 (H·м);

Mx3 = – RA·z3 + RB·(z3 – a) +M + q·(z3 – 2a) ·(z3 – 2a) /2 ;

         Mx3 (2a)= – 2,05·104 ·2· 0,8+ 2,45·10 4 · 0,8 +10 4 = – 3,2· 103  (H·м);

         Mx3 (3a) = – 2,05·104 ·3· 0,8+ 2,45·10 4 ·2· 0,8 +10 4 +104 ·0,82·0,5 ;

Mx3 (3a) = 3,2·103   (H·м);

Mx4 = – RA·z4 + RB·(z4 – a) +M + q · (z4 – 2a )·(z4 ­– 2a)/2 ­– P1(z4 – 3a) ;

         Mx4 (3a) = – 2,05·104 ·3· 0,8 + 2,45·10 4 ·2· 0,8 + 10 4  + 10 4  · 0,8 2 /2­

­  

          Mx4 (3a) = 3,2·103   (H·м);

Mx4 (4a) = – 2,05·104 ·4· 0,8 + 2,45·10 4 ·3· 0,8 + 10 4 + 10 4 · (2·0,8)2 ·0,5 ­–

–2·104 ·0,8 = 0.

Эпюры поперечных сил и  изгибающих моментов представлены на рисунке 1.3.

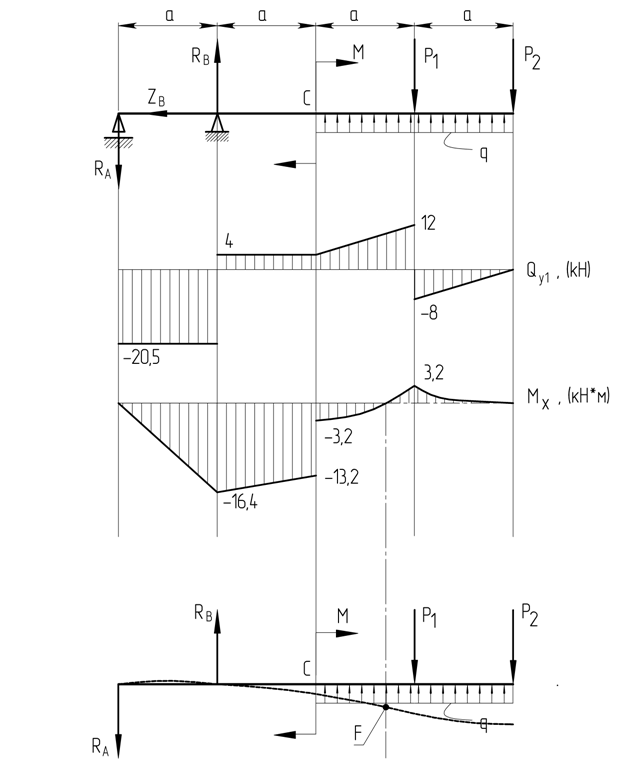
Рисунок 1.3

Точка F – точка перегиба

Условие прочности :

σmax =  ≤ [σ] ;

Отсюда :

         Wx =  = = 0,1025·10 –3 м3 = 102,5 см3.

         По ГОСТ 8239–72 выбираем двутавр № 16,имеющий Wx = 118 см3 . Недонапряжение балки составит  13,1 %.

Определим касательные напряжения в сечении с максимальным значением поперечной силы:

         τmax = = = 29,1 (МПа)

         Для составления уравнений перемещений поместим начало координат в левое крайнее сечение балки. Тогда уравнение прогибов (универсальное уравнение) для данной балки будет иметь вид:

         E· Ix · y = E·Ix·y0 + E·Ix· θ 0·z – RA·  │ + RB· │ + M·  +

+q· │ – P1· │.

         Начальными параметрами являются θ 0 ≠ 0 и у0 = 0 (угол поворота сечения и прогиб в начале системы координат, то есть в опоре А).     Значение θ 0 найдем из условия, что прогиб балки в точке В равен нулю:

уz=а = RB = 0.

Из уравнения прогибов имеем :

         0 = E·Ix· θ 0·0,8 ­– 2,05·104 ·  + 2,45·

­         θ 0 =  ;

Уравнение изогнутой оси балки имеет вид :

         E·Ix· у = 2,187·10 3·z – 2,05·104 · + 2,45·104· + 104 · +

Скачать файл