Решение 23 заданий с множествами и подмножествами (Вариант 31), страница 3

x	0	1	2	3	4	5	6	7	8	9	10	11	12
f1	0	1	3	6	6	10	11	13	13	15	15	17	23
f2	0	1	4	4	4	4	4	9	9	11	11	11	14
f3	0	2	2	2	2	3	3	7	8	9	10	11	13
f4	0	5	10	12	15	16	18	20	23	23	23	26	26

       Решение:

Одно из решений данной задачи является полный перебор, количество вариантов  при предположении, что все дни различны, 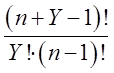, когда все дни одинаковы. Количество вариантов слишком велико при увеличении  и , поэтому требуется уменьшить число вариантов.

Запишем формулировку задачи в терминах целевой функции и ограничений.

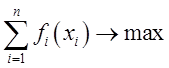 – целевая функция,

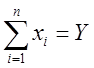 – ограничения или ресурс,

 – дополнительное ограничение,

 – план или решение.

Идея динамического программирования – решение задачи на -м шаге получаем через  шаг (рекуррентно). Введём функцию  – оптимальное значение целевой функции на -м шаге, очевидно, что  – оптимальное значение целевой функции всей задачи, то есть 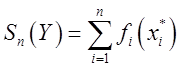. Рассмотрим задачу для  экзаменов.

              ,

              ,

              ,

              .

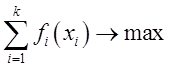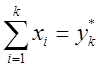Справедливо рекуррентное соотношение:

              , ;

              , , .

Найдём по данным формулам значения .

          ,           

              …

              .

             ,

                    ,

         

              …

            ,

          ,

              …

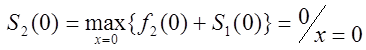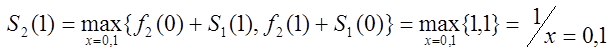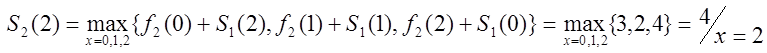
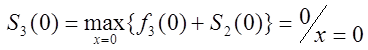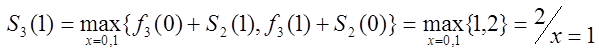x

0

1

2

3

4

5

6

7

8

9

10

11

12

f1

0

1

3

6

6

10

11

13

13

15

15

17

23

f2

0/0

1/0,1

4/2

6/0

7/1,2

10/0,2

11/0,1

14/2

15/2

17/2

17/2,3

19/2

23/0

f3

0/0

2/1

4/0

6/0,1

8/1

10/0

12/1

14/0

16/1

17/0,1

19/1

19/0,1,2

23/0

f4

0/0

5/1

10/2

12/2,3

15/4

17/4

19/4

21/4

23/4,8

25/4,8

27/4,8

29/4,8

31/4,8

18. Какая функция получается из g и h с помощью схемы примитивной рекурсии:

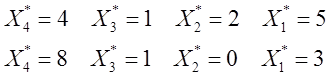
(а) g(x) = x, h(x,y,z) = z^x;

 f(x,0)=x

 f(x,1)=f(x,0)^x=x^x

 f(x,2)=f(x,1)^x=x^x*x

……………………………….

 f(x,y+1)=f(x,y)^x=x^x*x*…*x=x^y*x

=>f(x,y)=x^(y-1)*x

(б) g(x) = x, h(x,y,z) = x^z;

f(x,0)=x

f(x,1)=x^f(x,0)=x^x

………………………………..

f(x,y+1)=x^f(x,y)=

=>f(x,y)=

19. Доказать, что следующие функции примитивно рекурсивны:

(а)  – частное от деления x на y (здесь  = x);

=,

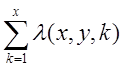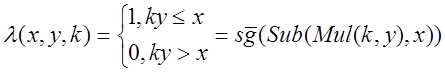
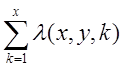=f(x,y,x)

f(x,y,1) =

……………………………...

f(x,y,z+1) = 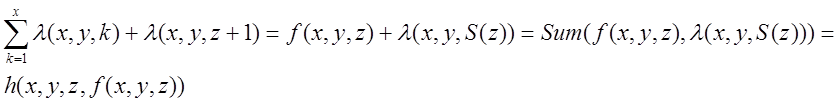Из этого следует , что f(x,y,z) - примитивно рекурсивнa ->= f(x,y,x) - примитивно рекурсивнa

(б) rest(x, y) – остаток от деления x на y (здесь rest(x, 0) = x);

rest(x, y) = x – y* = Sub(x,Mul(y, )) – композиция примитивно рекурсивных функций есть примитивно рекурсивнaя функция .

(в) t(x) – число делителей числа x, где t(0) = 0;

t(x) =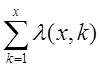

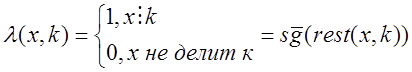
t(x) =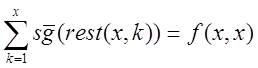

f(x,1 ) =

………………………………….

f(x,y+1) =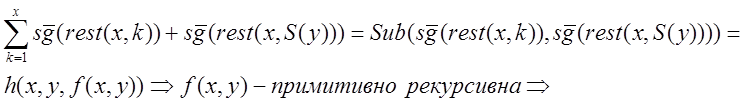

t(x) =f(x,x) = примитивно рекурсивна.

(г) s(x) – сумма делителей числа x, где s(0) = 0;