2) ![]() . По условию R2-симметричное
отношение®
. По условию R2-симметричное
отношение®![]()
Т.о. взяв произвольную пару множества R1ÇR2 , мы показали , что и в множестве R1 ,и в R2 одновременно , а значит в множестве R1ÇR2 , будет присутствовать пара <y,x> .ч.т.д.
А={1,2}
P={<1,1>,<2,2>,<1,2>}
1. рефлексивное : любое натуральное число делит само себя
2. транзитивное
: ![]() а,б,с
а,б,с![]() N если
N если ![]() и
и ![]() , то
, то ![]()
3. антисимметричное
: ![]() а,б
а,б![]() N если
N если ![]() и
и ![]() , то а=б
, то а=б
a) урны различны;
1ую урну можно выбрать m способами , 2ю – m-1 , 3ю - m – 2 и т.д.
Для первых m1 урн получаем
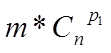 - выбираем первую урну и размещаем в нее p1 шаров из n .
- выбираем первую урну и размещаем в нее p1 шаров из n .
![]() для второй , но размещаем p1
шаров из оставшихся .
для второй , но размещаем p1
шаров из оставшихся .
………………………………………………………………………………………………
![]() - число способов выбрать m1
урну и положить в нее p1
- число способов выбрать m1
урну и положить в нее p1
шаров из оставшихся .
Для следующих m2 урн получаем :
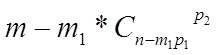 - для m1+1урны
.
- для m1+1урны
.
![]() для m1+2урны
.
для m1+2урны
.
………………………………………………………………………………………………
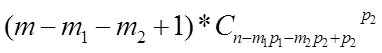 - для m1+
m2 урны.
- для m1+
m2 урны.
Т.о. ® для m урн :
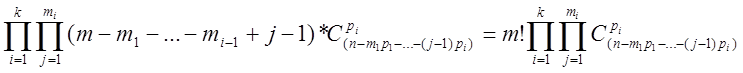
b) урны, содержащие одинаковое число шаров, неразличимы.
Решение отличается от а) лишь тем, что количество способов выбрать урны в каждой группе (m1, m2,…, mk) нужно разделить на число перестановок внутри группы (mi!) :
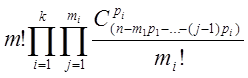
не менее двух задач по комбинаторике => задач по комбинаторике ≥2
C310*C215 + C210*C315 + C110*C415 + C-10*C515
C165!-выбираем место под четную , остальные 5 ставим как хотим .
 Сколько
диагоналей в выпуклом n-угольнике?
Сколько
диагоналей в выпуклом n-угольнике? При n ≥ 4
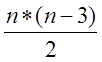 -n –выбираем вершину (n-3) – для
выбранной вершины выбираем вершину,
-n –выбираем вершину (n-3) – для
выбранной вершины выбираем вершину,
не смежную. Делим на 2 , потому что м посчитала диагонали по 2 раза .
![]()
![]() -всевозможные
способы выиграть m-партий из n-партий
-всевозможные
способы выиграть m-партий из n-партий
![]() –максимальное
число благополучных исходов для первого и второго игрока.
–максимальное
число благополучных исходов для первого и второго игрока.
n! – (n – m + 1)!m!
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.