


Пусть функция ![]() определена в некоторой окрестности
определена в некоторой окрестности ![]() . Тогда
. Тогда 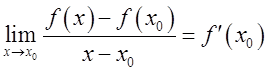 называют производной функции
в точке
называют производной функции
в точке ![]() . Если
вышеописанный предел равен нулю, то говорят, что функция имеет бесконечную
производную в точке
. Если
вышеописанный предел равен нулю, то говорят, что функция имеет бесконечную
производную в точке ![]() .
.
Если функция ![]() определена в некоторой право-
(лево-) сторонней окрестности точки
определена в некоторой право-
(лево-) сторонней окрестности точки ![]() и
существует конечный (бесконечный) передел определенного знака, то
и
существует конечный (бесконечный) передел определенного знака, то 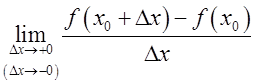 называют соответственно конечной
(бесконечной) правой (левой) производной функции
называют соответственно конечной
(бесконечной) правой (левой) производной функции ![]() в точке
в точке ![]() :
: ![]() . Замечание:
Функция
. Замечание:
Функция ![]() , определенная в
окрестности точки
, определенная в
окрестности точки ![]() имеет
производную в этой точке тогда и только тогда, когда
имеет
производную в этой точке тогда и только тогда, когда ![]() .
.
Функция ![]() называется дифференцируемой
в точке
называется дифференцируемой
в точке ![]() , если она
определена в некоторой окрестности точки
, если она
определена в некоторой окрестности точки ![]() и ее приращение
и ее приращение ![]() , где
, где ![]() - функция от переменной
- функция от переменной ![]() называется дифференциалом
функции
называется дифференциалом
функции ![]() в точек
в точек ![]() и обозначается
и обозначается ![]() .
. ![]() обычно обозначают
обычно обозначают ![]() и записывают дифференциал функции в
виде
и записывают дифференциал функции в
виде ![]() . Замечание: Величина
. Замечание: Величина ![]() является бесконечно малой более
высокого порядка, чем
является бесконечно малой более
высокого порядка, чем ![]() .
.
Теорема о дифференцировании
функции. Для того, чтобы функция ![]() была дифференцируема в
некоторой точке
была дифференцируема в
некоторой точке ![]() необходимо и достаточно, чтобы
она имела в этой точке производную, при этом
необходимо и достаточно, чтобы
она имела в этой точке производную, при этом ![]() . Замечание: Дифференцируемость
функции
. Замечание: Дифференцируемость
функции ![]() в точке
в точке ![]() равносильно существованию в этой
точке конечной производной.
равносильно существованию в этой
точке конечной производной.
Теорема о непрерывности
дифференцируемой функции. Если функция ![]() дифференцируема в некоторой точке,
то она непрерывна в этой точке. Следствие: Если функция в некоторой точке имеет
конечную производную, то она непрерывна в этой точке, обратное не всегда верно.
дифференцируема в некоторой точке,
то она непрерывна в этой точке. Следствие: Если функция в некоторой точке имеет
конечную производную, то она непрерывна в этой точке, обратное не всегда верно.
Если существует конечный ![]() , то прямая, уравнение которой имеет
вид
, то прямая, уравнение которой имеет
вид![]() , полученная из уравнения
прямой
, полученная из уравнения
прямой ![]() при
при ![]() , называется касательной к графику
функции в точке
, называется касательной к графику
функции в точке ![]() . Получаем, что
. Получаем, что ![]() . Дифференциал в точке
. Дифференциал в точке
![]() равен приращению ординаты
касательной в соответствующей точке графика функции.
равен приращению ординаты
касательной в соответствующей точке графика функции.
Пусть функция ![]() определена в некоторой
определена в некоторой ![]() . Будем называть
. Будем называть  скоростью
изменения переменой
скоростью
изменения переменой ![]() относительно переменной
относительно переменной
![]() в точке
в точке ![]() .
.
Правила вычисления производных.
Пусть ![]() и
и ![]() определены в некоторой
определены в некоторой ![]() , и в точке
, и в точке ![]() существуют их производные. Тогда
функции
существуют их производные. Тогда
функции  тоже имеют
производные на
тоже имеют
производные на ![]() причем: 1)
причем: 1)  ; 2)
; 2) 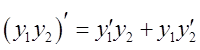 ; 3)
; 3) 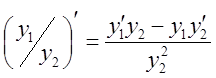 . Следствия: 1) Если функция
. Следствия: 1) Если функция ![]() имеет производную в точке
имеет производную в точке ![]() , то функция
, то функция ![]() тоже имеет производную в этой
точке, равную
тоже имеет производную в этой
точке, равную  ; 2) Если
функции
; 2) Если
функции ![]() имеют в точке
имеют в точке ![]() производные, то любая линейная
комбинация этих функций тоже будет иметь производную
производные, то любая линейная
комбинация этих функций тоже будет иметь производную 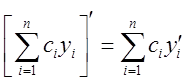 ; 3) Аналогичные свойства
выполняются для дифференциалов функции: 1.
; 3) Аналогичные свойства
выполняются для дифференциалов функции: 1. ![]() ; 2.
; 2. ![]() ; 3.
; 3. 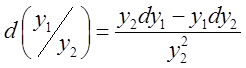 ; 4.
; 4. ![]() .
.
Теорема о производной обратной
функции. Пусть функция ![]() непрерывна
и строго монотонна в некоторой
непрерывна
и строго монотонна в некоторой ![]() и
пусть в этой точке существует
и
пусть в этой точке существует 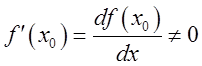 . Тогда
обратная функция
. Тогда
обратная функция ![]() имеет
производную в точке
имеет
производную в точке ![]() , причем
производная обратной функции равна обратной производной прямой функции
, причем
производная обратной функции равна обратной производной прямой функции 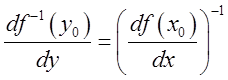 .
.
Теорема о производной сложной
функции. Пусть функция ![]() имеет
производную в точке
имеет
производную в точке ![]() , а функция
, а функция ![]() имеет производную в точке
имеет производную в точке ![]() . Тогда сложная функция
. Тогда сложная функция ![]() также имеет производную в точке
также имеет производную в точке ![]() .
.
Замечания: 1) Аналогичные
соотношения выполняются для дифференциалов: ![]() ; 2. Свойства инвариантности формы
первого дифференциала относительно преобразования независимых переменных:
; 2. Свойства инвариантности формы
первого дифференциала относительно преобразования независимых переменных: ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
||||||||||||||||
|
|
|
||||||||||||||||
Пусть функция ![]() определена на интервале
определена на интервале ![]() и имеет в каждой точке этого
интервала производную
и имеет в каждой точке этого
интервала производную ![]() .
Если в некоторой точке
.
Если в некоторой точке ![]() функция
дифференцируема, то
функция
дифференцируема, то ![]() называется второй
производной функции
называется второй
производной функции ![]() в
точке
в
точке ![]() :
: 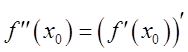 . Аналогично определяется производная
. Аналогично определяется производная
![]() -ого порядка:
-ого порядка:  .
.
Функция называется ![]() раз непрерывно дифференцируемой
на некотором промежутке, если во всех точках этого промежутка она имеет
непрерывные производные до порядка
раз непрерывно дифференцируемой
на некотором промежутке, если во всех точках этого промежутка она имеет
непрерывные производные до порядка ![]() включительно.
включительно.
Свойства вторых производных.
1) Пусть функция ![]() имеет вторую
производную в точке
имеет вторую
производную в точке ![]() , а функция
, а функция ![]() имеет вторую производную в точке
имеет вторую производную в точке ![]() . Тогда сложная функция
. Тогда сложная функция ![]() имеет в точке
имеет в точке ![]() вторую производную, которая
вычисляется по формуле
вторую производную, которая
вычисляется по формуле ![]() . 2) Функция
. 2) Функция
![]() непрерывна и строго
монотонна в некоторой
непрерывна и строго
монотонна в некоторой ![]() и
пусть в этой окрестности
и
пусть в этой окрестности ![]() . Тогда
обратная функция
. Тогда
обратная функция ![]() имеет вторую
производную в точке
имеет вторую
производную в точке ![]() , причем она
может быть вычислена по формуле
, причем она
может быть вычислена по формуле 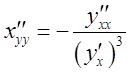 .
.
Правило дифференцирования
параметрически заданных функций. Пусть ![]() , и они определены в некоторой
, и они определены в некоторой ![]() . Причем одна из них, например
функция
. Причем одна из них, например
функция ![]() непрерывна и
строго монотонна в этой окрестности. Тогда для функции
непрерывна и
строго монотонна в этой окрестности. Тогда для функции ![]() и тогда в
и тогда в ![]() . Если функции
. Если функции ![]() имеют в производные в точке
имеют в производные в точке ![]() и если
и если ![]() , то параметрически заданная функция
, то параметрически заданная функция
![]() имеет в этой точке
производную, которая вычисляется по формуле
имеет в этой точке
производную, которая вычисляется по формуле 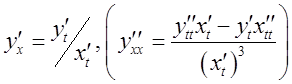 .
.
Значение дифференциала ![]() , т.е. дифференциала от первого
дифференциала, в точке
, т.е. дифференциала от первого
дифференциала, в точке ![]() называется
вторым дифференциалом функции:
называется
вторым дифференциалом функции: ![]() .
Дифференциал n-ого порядка вычисляется
аналогично:
.
Дифференциал n-ого порядка вычисляется
аналогично: ![]() . Замечание:
Второй дифференциал в отличие от первого не обладает свойством инвариантности
относительно свободного переменного:
. Замечание:
Второй дифференциал в отличие от первого не обладает свойством инвариантности
относительно свободного переменного: 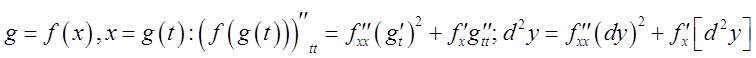 .
.
Теоремы о среднем
дифференцируемых функций. Теорема Ферма. Пусть функция ![]() определена в некоторой
определена в некоторой ![]() и принимает в этой точке наибольшее
или наименьшее значение, тогда если при
и принимает в этой точке наибольшее
или наименьшее значение, тогда если при ![]() существует конечная (бесконечная
определенного знака) производная, то она равна нулю. Теорема Ролля.
Пусть функция
существует конечная (бесконечная
определенного знака) производная, то она равна нулю. Теорема Ролля.
Пусть функция ![]() : 1) непрерывна
на
: 1) непрерывна
на ![]() ; 2) имеет в каждой точке
; 2) имеет в каждой точке ![]() конечную или бесконечную
определенного знака производную; 3) принимает
конечную или бесконечную
определенного знака производную; 3) принимает ![]() . Тогда
. Тогда ![]() . Теорема Лагранжа. Если
функция
. Теорема Лагранжа. Если
функция ![]() непрерывна на
непрерывна на ![]() и в каждой точке принадлежащей
этому интервалу имеет конечную или определенного знака бесконечную производную,
то в этом интервале существует, по крайней мере, одна точка
и в каждой точке принадлежащей
этому интервалу имеет конечную или определенного знака бесконечную производную,
то в этом интервале существует, по крайней мере, одна точка ![]() . Теорема Коши. Пусть даны
функции
. Теорема Коши. Пусть даны
функции ![]() , и для них
выполнены следующие условия: 1) обе функции непрерывны на
, и для них
выполнены следующие условия: 1) обе функции непрерывны на ![]() ; 2) обе функции имеют производные в
любой точке этого интервала; 3)
; 2) обе функции имеют производные в
любой точке этого интервала; 3) ![]() . Тогда
. Тогда
 .
.
Выражения вида 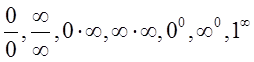 называются неопределенностями.
называются неопределенностями.
Теорема. Пусть функции ![]() , определенные на
, определенные на ![]() таковы, что: 1)
таковы, что: 1) ![]() ; 2)
; 2) ![]() . Тогда
существует
. Тогда
существует 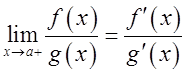 . Тогда правилом
Лопеталя будет называть определение предела отношений функций по формуле
. Тогда правилом
Лопеталя будет называть определение предела отношений функций по формуле 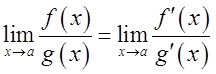 (
(![]() может
быть равно
может
быть равно ![]() ). Это правило
справедливо для неопределенностей вида
). Это правило
справедливо для неопределенностей вида 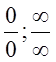 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.