





Министерство общего и профессионального образования
Российской Федерации
Новосибирский государственный технический университет
"Дифференциальные уравнения"
Вариант №7
Группа: ПМи- 41
Студент: Крицин К.А.
Преподаватель: Баландин М.Ю.
Новосибирск
2006
I. Определить тип дифференциальных уравнений и решить:
1) 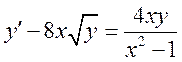
2) 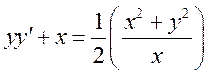
3) ![]()
4) ![]()
Решение:
1)
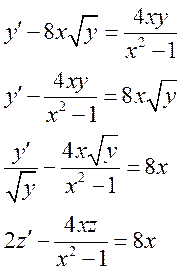
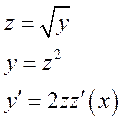
Методом вариации постоянных:
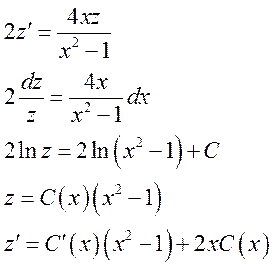
Подставляем в исходное:
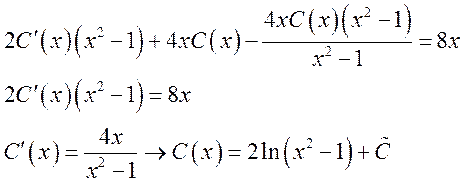
Ответ: ![]()
2)
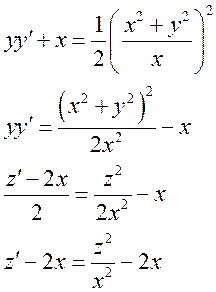
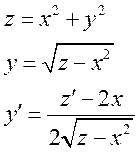
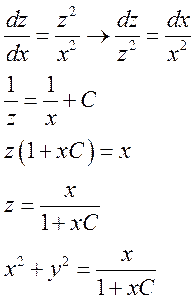
Ответ: 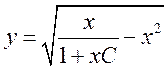
3) (Уравнение Клеро)
![]()
![]()
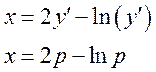
Уравнение можно разрешить относительно х:
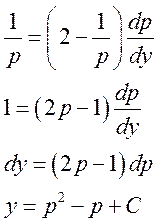
Ответ: ![]()
4)
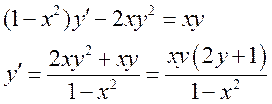
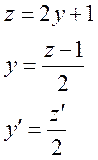
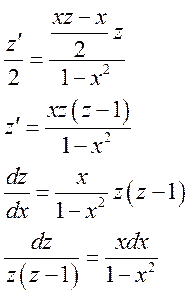
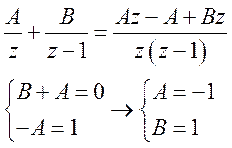
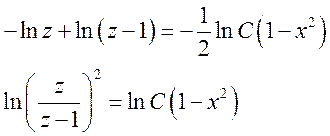
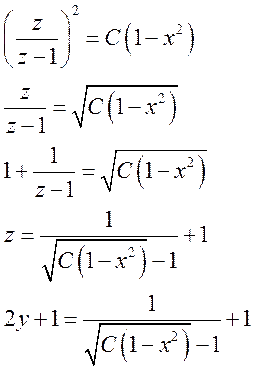
Ответ: 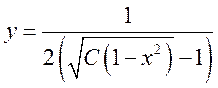
II.
Решить систему линейных
неоднородных дифференциальных уравнений вида 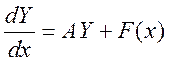 методом
вариации постоянных (все вычисления, преобразования и упрощения выполнялись с
помощью программы MathCAD):
методом
вариации постоянных (все вычисления, преобразования и упрощения выполнялись с
помощью программы MathCAD):
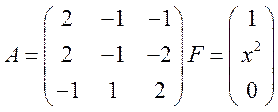
Найдем собственные значения матрицы А. Поскольку
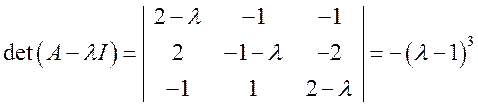 ,
,
матрица
А имеет только одно собственное значение ![]() . Его
алгебраическая кратность
. Его
алгебраическая кратность ![]() . Выясним какова
геометрическая кратность
. Выясним какова
геометрическая кратность ![]() .
.
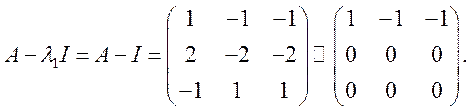
Геометрическая
кратность собственного значения ![]() равна
равна
![]()
Поскольку
геометрическая кратность ![]() меньше алгебраической,
матрица А не является матрицей простой структуры (А – дефектная
матрица).
меньше алгебраической,
матрица А не является матрицей простой структуры (А – дефектная
матрица).
В силу того, что A имеет
только одно собственное значение, трехмерное пространство X, в
котором действует линейный оператор совпадает с корневым подпространством ![]() . Это подпространство разложимо в прямую
сумму двух циклических подпространств размерности 2 и 1. Таким образом, искомый
жорданов базис состоит из двух собственных векторов и одного присоединенного
вектора первого порядка.
. Это подпространство разложимо в прямую
сумму двух циклических подпространств размерности 2 и 1. Таким образом, искомый
жорданов базис состоит из двух собственных векторов и одного присоединенного
вектора первого порядка.
Найдем собственные векторы ![]() , решая
однородную СЛАУ
, решая
однородную СЛАУ
![]()
В
качестве свободных переменных возьмем ![]() и
и ![]() . Тогда
. Тогда ![]() и
и ![]() .
.
Для
построения жорданова базиса осталось найти присоединенный вектор первого
порядка ![]() . Решим неоднородную систему уравнений
. Решим неоднородную систему уравнений ![]()
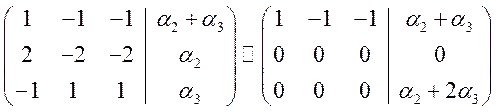 .
.
Система
будет совместна только тогда, когда ![]() . Подставив это условие
в выражение для
. Подставив это условие
в выражение для ![]() , получим общий вид собственных
векторов, имеющих присоединенные векторы первого порядка:
, получим общий вид собственных
векторов, имеющих присоединенные векторы первого порядка: ![]() .
.
Найдем
общий вид присоединенных векторов в зависимости от значения ![]() , для чего продолжим решение системы
, для чего продолжим решение системы
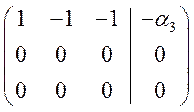 .
.
В
качестве свободных переменных возьмем ![]() и
и ![]() . Тогда
. Тогда ![]() и
и ![]() .
.
Подставим
в изначальное выражение для ![]() значения
значения ![]() и
и ![]() ,
получим первый собственный вектор
,
получим первый собственный вектор ![]() . Для второго
собственного вектора и присоединенного к нему подставим:
. Для второго
собственного вектора и присоединенного к нему подставим: ![]() , и оставим
, и оставим ![]() .
Получим:
.
Получим: ![]() и
и ![]() .
Составляем Р и находим J:
.
Составляем Р и находим J:
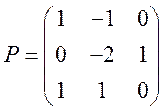
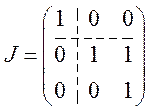
Общее
решение однородной системы ![]() , где
, где 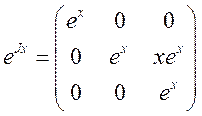 :
:
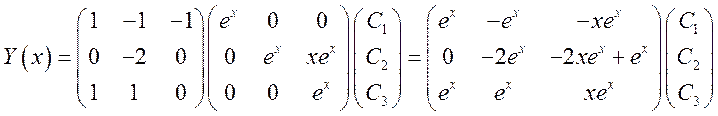
Фундаментальная
система решений: 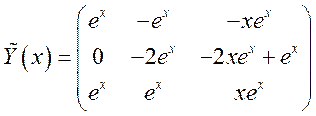 . Тогда решение неоднородной
системы ДУ
. Тогда решение неоднородной
системы ДУ ![]() ,
, ![]() .
.
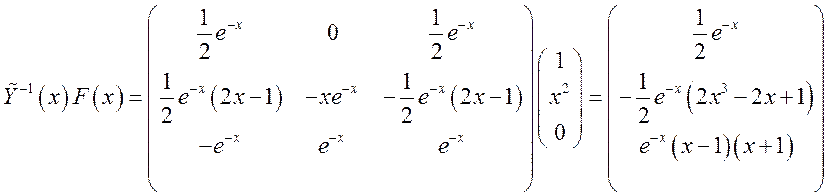 . Тогда
. Тогда 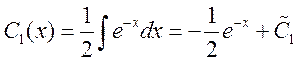 ,
,
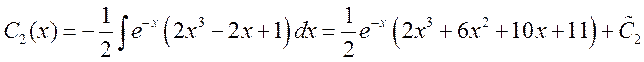 ,
, ![]()
Общее решение неоднородной линейной системы ДУ:
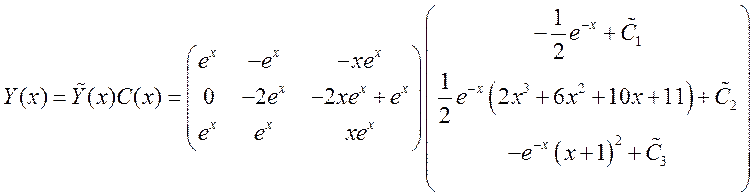
III. Решить неоднородное дифференциальное уравнение n-го порядка методом вариации постоянных (все вычисления, преобразования и упрощения выполнялись с помощью программы MathCAD):
![]() ,
, ![]()
![]()
![]()
![]()
Т.к.
корень ![]() имеет кратность 2, то:
имеет кратность 2, то:
![]()
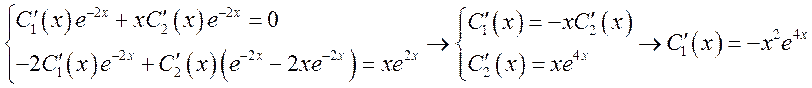
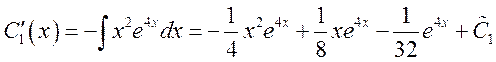
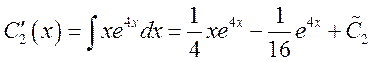
Ответ:
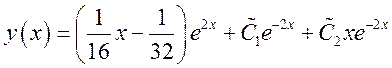
![]()
![]()
![]()
![]()
![]()
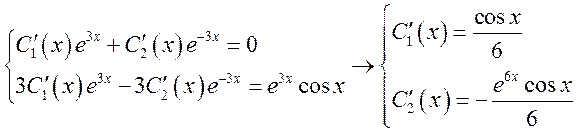
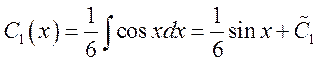
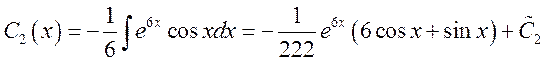
Ответ: 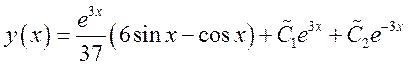
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.