= (a+(c+e),b+(d+f)) =
(a,b)+(c+e,d+f) = (a,b)+[(c,d)+(e,f)]= ![]() +(
+(![]() +
+![]() ).
).
3. Существование нуля:
![]() =(x,y);
=(x,y);
![]() +
+![]() = (a,b)+(x,y) = (a+x,b+y) =
= (a,b)+(x,y) = (a+x,b+y) = ![]() = (a,b);
= (a,b);
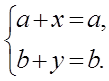
Отсюда х=0, у=0 и ![]() =(0,0)
=(0,0)![]() C .
C .
4. Существование противоположного элемента:
(–![]() )=(x,y);
)=(x,y);
![]() +(–
+(–![]() ) = (a,b)+(x,y)
= (a+x,b+y)=
) = (a,b)+(x,y)
= (a+x,b+y)=![]() =(0,0);
=(0,0);
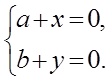
Отсюда x = –a, y = –b и –![]() = (–a, –b)
= (–a, –b) ![]() C .
C .
B. Аксиомы умножения.
1. Коммутативность умножения:
![]() =
(a,b)(c,d) = (ac – bd,ad+bc);
=
(a,b)(c,d) = (ac – bd,ad+bc);
![]() =
(c,d)(a,b) = (ca – db,cb+da)= (ac – bd,ad+bc) =
=
(c,d)(a,b) = (ca – db,cb+da)= (ac – bd,ad+bc) = ![]() .
.
2. Ассоциативность умножения:
![]() =
[(a,b)(c,d)](e,f) = (ac–bd, ad+bc)(e,f) = ((ac–bd)e–(ad+bc)f,(ac–
=
[(a,b)(c,d)](e,f) = (ac–bd, ad+bc)(e,f) = ((ac–bd)e–(ad+bc)f,(ac–
–bd)f+(ad+bc)e) = (ace – bde – adf – bcf, acf+ade+bce – bdf);
![]() = (a,b)[(c,d)(e,f)]= (a,b)(ce – df, cf+ed) = (a(ce –
df) – b(cf+ed), b(ce –
= (a,b)[(c,d)(e,f)]= (a,b)(ce – df, cf+ed) = (a(ce –
df) – b(cf+ed), b(ce –
–df)+a(cf+ed)) = (ace – adf – bcf – bcd,
acf+aed+bce – bdf) = ![]() ;
;
3. Существование единичного элемента
1 = (x,y);
1![]() =
(x,y)(a,b) = (xa – yb, xb+ya) =
=
(x,y)(a,b) = (xa – yb, xb+ya) = ![]() =
(a,b);
=
(a,b); ![]() C
C
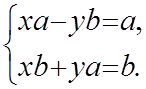
Из 2-го уравнения y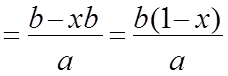 , a
, a![]() 0. Подставляем
в 1-е уравнение
0. Подставляем
в 1-е уравнение
xa – yb = xa – 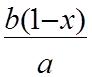 b = ax+
b = ax+![]() x
–
x
– ![]() =(a+
=(a+![]() )x
–
)x
–![]() = a;
= a;
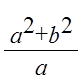 x
=
x
= 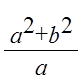 ;
;
x = 1; y =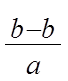 =
0;
=
0;
1 = (1,0) ![]() C
C
4. Существование обратного элемента:
![]() =
(x,y);
=
(x,y);
![]() =
(a,b)(x,y) = (ax – by, ay+bx) = 1 = (1,0);
=
(a,b)(x,y) = (ax – by, ay+bx) = 1 = (1,0);
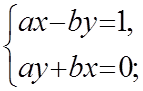
Из 2-го уравнения y = – ![]() x, a
x, a![]() 0. Подставим
в 1-е уравнение:
0. Подставим
в 1-е уравнение:
ax – by = ax – b(–![]() x)
= ax+
x)
= ax+![]() x
=
x
= 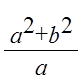 x
= 1;
x
= 1;
x
= 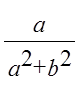 ;
;
y
= – ![]() x = –
x = – ![]()
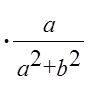 = –
= – 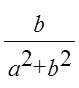 ;
;
![]() = (
= (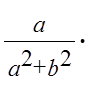 –
– 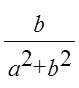 ) )
) )![]() C.
C.
C. Дистрибутивность умножения относительно сложения:
![]() =
(a,b)[(c,d)+(e,f)] = (a,b)(c+e, d+f) = (a(c+e)–b(d+f), b(c+e)+a(d+f))=
=
(a,b)[(c,d)+(e,f)] = (a,b)(c+e, d+f) = (a(c+e)–b(d+f), b(c+e)+a(d+f))=
= (ac+ae – bd – bf, bc+be+ad+af);
![]() =
(a,b)(c,d)+(a,b)(e,f) = (ac – bd, ad+bc)+(ae – bf, af+be) =
=
(a,b)(c,d)+(a,b)(e,f) = (ac – bd, ad+bc)+(ae – bf, af+be) =
= (ac+ae – bd – bf,
ad+bc+af+be) = ![]() .
.
Таким образом, множество комплексных чисел Cявляется полем.
Положим
i = (0,1);
i2 = (0,1)![]() (0,1)
= (0 – 1, 0+0) = (-1,0);
(0,1)
= (0 – 1, 0+0) = (-1,0);
![]() =
(a,b) = (a,0)+(0,b) = a(1,0)+b(0,1) = a+bi;
=
(a,b) = (a,0)+(0,b) = a(1,0)+b(0,1) = a+bi;
 |
![]() = a+bi– запись
комплексного числа в алгебраической форме, причем
= a+bi– запись
комплексного числа в алгебраической форме, причем
a
= Re![]() – действительная
часть числа
– действительная
часть числа ![]() ;
;
b
= Im![]() – мнимая
часть
– мнимая
часть ![]() .
.
Действия над комплексными числами, записанными в алгебраической форме:
(a+bi)+(c+di) = (a+c)+(b+d)i;
(a+bi) – (c+di) = (a – c)+(b – d)i;
(a+bi)(c+di) = (ac – bd)+(ad+bc)i;
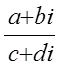 =
= 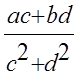 +
+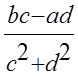 i.
i.
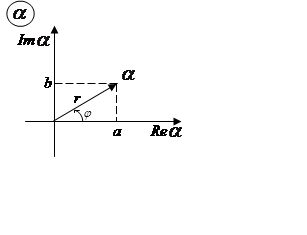 Комплексные числа
принято изображать на комплексной плоскости:
Комплексные числа
принято изображать на комплексной плоскости:
|
Если ![]() ,
то arg
,
то arg![]() =
=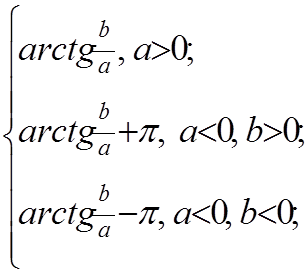
![]() =
a+bi = rcos
=
a+bi = rcos![]() +irsin
+irsin![]() =
r(cos
=
r(cos![]() +isin
+isin![]() )
)

![]() = r(cos
= r(cos![]() +isin
+isin![]() ) –запись комплексного числа в тригонометрической форме.
) –запись комплексного числа в тригонометрической форме.
Перемножим два комплексных числа в тригонометрической форме
![]() =[
=[![]() (cos
(cos![]() +isin
+isin![]() )][
)][![]() (cos
(cos![]() +isin
+isin![]() )]=
)]=![]() [(cos
[(cos![]() cos
cos![]() –sin
–sin![]() sin
sin![]() )+
)+
+i(sin![]() cos
cos![]() –cos
–cos![]() sin
sin![]() )]=
)]=
![]() [cos(
[cos(![]() +
+![]() )+isin(
)+isin(![]() +
+![]() )],
т.е.
)],
т.е.
 |
|![]() | = |
| = |![]() |
|![]() |
|![]() |,
|,
arg(![]() ) = arg
) = arg![]() +arg
+arg![]() .
.
Выполним деление комплексных чисел в тригонометрической форме
![]() =
=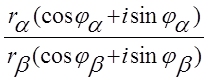 =
=
![]()
![]()
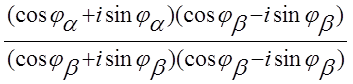 =
=
= ![]()
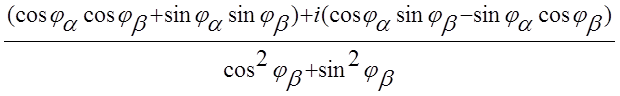 =
=
=![]() [cos(
[cos(![]() )+isin(
)+isin(![]() )].
)].
Отсюда
 |
![]() =
= ![]() ,
,
arg(![]() ) = arg
) = arg![]() – arg
– arg![]() .
.
Число ![]() = a
– bi сопряжено
к числу
= a
– bi сопряжено
к числу ![]() = a+bi,
= a+bi,
|![]() |= |
|= |![]() |, arg
|, arg![]() = – arg
= – arg![]() .
.
Сумма и произведение комплексно сопряженных чисел являются действительными числами.
Можно показать, что
![]() =
=
![]() +
+![]() ,
, ![]() +
+
![]() =
2a;
=
2a;
![]() =
=
![]() –
–![]() ,
,
![]()
![]() =
a2+b2 = |
=
a2+b2 = |![]() |2;
|2;
![]() =
=
![]()
![]() ,
, ![]() -1 = r
-1(cos(–
-1 = r
-1(cos(–![]() )+isin(–
)+isin(–![]() )).
)).
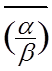 =
=![]() ;
;
Заметим, что сумма в определителе имеет n! слагаемых. Действительно, i1можно
выбрать n способами, i2 – (n–1) способом, …, n! = n![]() (n–1)
(n–1) ![]() …
…![]() 2
2![]() 1.
1.
Таким образом, определитель Dсостоит из n! членов вида (1), которые берутся со знаком «+», если N(i1, i2, …, in) четно, и со знаком «–», если N(i1, i2, …, in) нечетно.
Примеры
1. 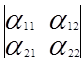 =
=
![]() 11
11![]() 22
(-1)N(1,2) +
22
(-1)N(1,2) + ![]() 21
21![]() 12
(-1)N(2,1) =
12
(-1)N(2,1) = 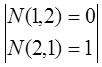 =
=![]() 11
11![]() 22 –
22 –![]() 21
21![]() 12.
12.
2. 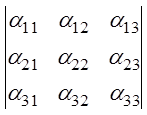 =
=
![]() 11
11![]() 22
22![]() 33 (–1)N(1,2,3
) +
33 (–1)N(1,2,3
) + ![]() 11
11![]() 32
32![]() 23 (–1)N(1,3,2)
+
23 (–1)N(1,3,2)
+
+![]() 21
21![]() 12
12![]() 33(–1)N(2,1,3)
+
33(–1)N(2,1,3)
+ ![]() 21
21![]() 32
32![]() 13 (–1)N(2,3,1)
+
13 (–1)N(2,3,1)
+ ![]() 31
31![]() 12
12![]() 23
23 ![]()
![]()
![]() (–1)N(3,1,2) +
(–1)N(3,1,2) +![]() 31
31![]() 22
22![]() 13 (-1)N(3,2,1)
=
13 (-1)N(3,2,1)
= 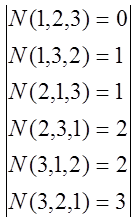 =
=![]() 11
11![]() 22
22![]()
![]() 33 –
–
33 –
–![]() 11
11![]() 32
32![]() 23 –
23 – ![]() 21
21![]() 12
12![]() 33 +
33 +![]() 21
21![]() 32
32![]() 13 +
13 + ![]() 31
31![]() 12
12![]() 23 –
23 – ![]() 31
31![]() 22
22![]() 13.
13.
Правило треугольников:
|
«+» |
«–» |
|
|
|
Замечание к правилу определения знака члена определителя
В соответствии с нумерацией элементов матриц будем
считать положительными направлениями для строк – слева направо, для столбцов – сверху
вниз. Отрезки, соединяющие два каких-либо элемента матриц, также могут
указывать направления: будем говорить, что отрезок, соединяющий элемент ![]() ij с элементом
ij с элементом ![]() kl, имеет положительный
наклон, если его правый конец расположен ниже левого, и отрицательный наклон,
если его правый конец лежит выше, чем левый. Мысленно проведем все отрезки,
соединяющие попарно элементы
kl, имеет положительный
наклон, если его правый конец расположен ниже левого, и отрицательный наклон,
если его правый конец лежит выше, чем левый. Мысленно проведем все отрезки,
соединяющие попарно элементы ![]() ,
, ![]() , …,
, …, ![]() произведения (1), имеющие отрицательный наклон
произведения (1), имеющие отрицательный наклон
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.