Синтез моделей фильтров

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Таганрогский Технологический институт

Южного Федерального университета

Лабораторная работа №3

по курсу УПиОСвСПРС

«Синтез моделей фильтров»

Выполнил:

Рудь Д. Е.

Проверил:

Шеболков В. В.

Таганрог 2008

Синтез рекурсивных фильтров по аналоговому прототипу

Необходимо синтезировать эллиптический дискретный ФВЧ с частотой среза 15 кГц из аналогового прототипа 2-мя методами:

1.  методом инвариантной ИХ

2.  методом билинейного z-преобразования.

Затем сравнить ЧХ и ИХ полученных фильтров и сделать выводы.

%эллиптический фильтр ВЧ

F0=180e3;                         

Fd=180e3;                          %частота дискретизации

Fp=16e3; Fs=14e3;

Wp=Fp/F0; Ws=Fs/F0;               %границы полос пропускания и задерживания (нормированные к частоте Найквиста)

Rp=1; Rs=30;                    %уровни пульсации в полосе пропускания и заграждения

[n,wc]=ellipord(Wp,Ws,Rp,Rs,'s'); %расчет порядка фильтра и частоты среза фильтра

[z,p,k]=ellipap(n,Rp,Rs);         %расчет нулей и полюсов

[b,a]=zp2tf(z,p,k);               %вычисление коэф-тов числителя и знаменателя передаточной функции фильтра-прототипа

Wc=wc*F0*2*pi;                    %частота среза в рад/с

[bt,at]=lp2hp(b,a,Wc);            %коэф-ты аналогового фильтра

[bz1,az1]=impinvar(bt,at,Fd);       % цифровой фильтр - инвариантность имп. хар

[bz2,az2]=bilinear(bt,at,Fd);       % цифровой фильтр – билинейн. преобр.

f=0:1:F0;

hs=freqs(bt,at,2*pi*f);              % частотная хар-ка аналогового фильтра

ns=1024;                            

[hz1,wz]=freqz(bz1,az1,ns,'whole'); % частотная хар-ка цифр. фильтра [bz1,az1]

hz2=freqz(bz2,az2,ns,'whole');    %частотная хар-ка цифр. фильтра [bz2,az2]

plot(f,abs(hs)),grid,xlabel('f,Hz');                     % -вывод частотных хар-к

hold on

plot(wz*F0/2/pi,abs(hz1),'--'),grid;

hold on

plot(wz*F0/2/pi,abs(hz2),':'),grid;

hold off

xlim([0 30e3])

grid on

figure

g1=impz(bz1,az1,50);                     % -вывод импульсных хар-к

stem(1:50,g1)

figure

g1=impz(bz2,az2,50);

stem(1:50,g1)

ЧХ полученных фильтров:

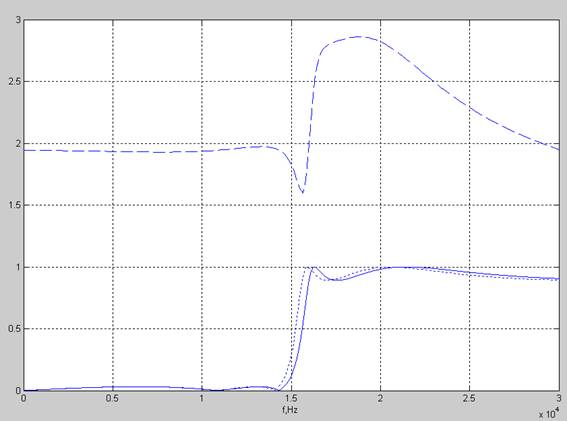
Рис. 1. Частотные характеристики фильтров: сплошная – аналоговый прототип, пунктир – цифровой, полученный методом инвариантной ИХ, точками - цифровой, полученный методом билинейного z-преобразования

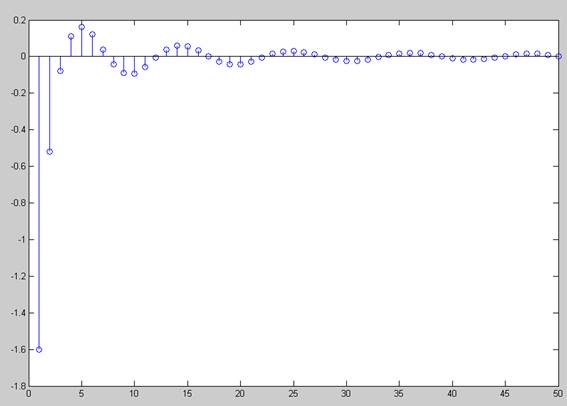
Рис. 2. ИХ дискретного фильтра, полученного методом инвариантной ИХ

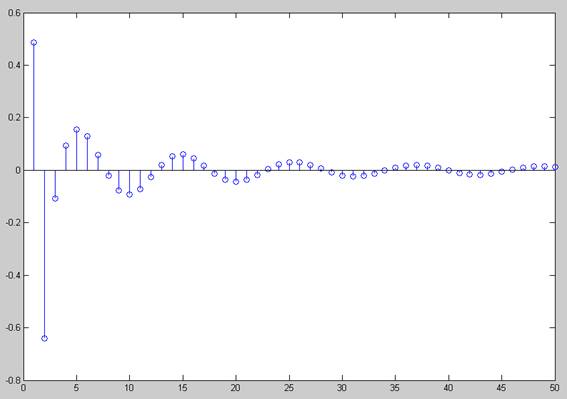
Рис. 3. ИХ дискретного фильтра, полученного методом билинейного z-преобразования

Как видно из ЧХ, нельзя синтезировать ФВЧ (и РФ) методом инвариантной ИХ, т. к. коэффициент передачи аналогового прототипа должен быть пренебрежительно малым на частотах, превышающих частоту Найквиста.

Simulink – модель для испытания фильтров

Построим Simulink-модель для анализа временных характеристик синтезированных дискретных фильтров. Будем подавать сигнал с частотами 8 и 21 кГц.