Цель работы: освоить технологию разработки аналоговых фильтров в системе MatLab
При разработке фильтров, как правило, задаются следующие параметры:
1)частотные границы полос пропускания ωp и задерживания ωs;
2) неравномерность АЧХ в полосе пропускания Rp и в полосе задерживания Rs (рис.1).

Рис.1
Аналоговые фильтры обычно разрабатываются следующим образом:
1) выбирается тип функции, аппроксимирующей частотную характеристику фильтра (Баттервортовская, Чебышевская, Бесселевская и т.п);
2) рассчитывается порядок ФНЧ-прототипа фильтра, его нули, полюса и коэффициенты передаточной функции;
3) выполняется процедура частотного преобразования ФНЧ-прототипа в требуемый тип фильтра (ФНЧ-ФНЧ, ФНЧ-ФВЧ, ФНЧ-ПФ, ФНЧ-РФ);
4) передаточная функция фильтра преобразуется к виду, удобному для его реализации.
1) Баттервортовские фильтры имеют частотную характеристику, которая описывается функцией
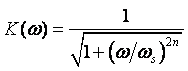
где ωs – частота среза фильтра, n – целое число, называемое порядком фильтра.
Коэффициент передачи фильтра на нулевой частоте равен 1, на частоте среза ≈ 0,707 = -3дБ независимо от порядка фильтра. АЧХ такого фильтра является максимально плоской при ω=0 и ω→∞ и монотонно спадает от 1 до 0 с ростом ω.
2) Чебышевские фильтры характеризуются двумя типами частотных характеристик.
Чебышевские фильтры первого рода (их иначе называют прямыми чебышевскими фильтрами) имеют частотную характеристику, которая описывается функцией
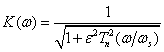 ,
,
где ε – параметр, определяющий величину пульсаций АЧХ в полосе пропускания;
Tn(x) – полином Чебышева n - го порядка.
АЧХ
чебышевского фильтра первого рода в полосе пропускания колеблется в пределах (![]() , 1), а вне полосы пропускания
монотонно стремится к нулю.
, 1), а вне полосы пропускания
монотонно стремится к нулю.
Параметр Rp и уровень пульсаций εсвязаны следующим образом:
![]()
Чебышевские фильтры второго рода (их иначе называют инверсными чебышевскими фильтрами) имеют частотную характеристику, которая описывается функцией
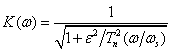 ,
,
где ε – параметр, определяющий величину пульсаций АЧХ в полосе задержания.
АЧХ
чебышевского фильтра второго рода в полосе задержания колеблется в пределах (0,
![]() ), а полосе пропускания монотонно
затухает.
), а полосе пропускания монотонно
затухает.
Параметр Rs и уровень пульсаций εсвязаны следующим образом:
![]()
Фильтр Чебышева по сравнению с фильтром Баттерворта того же порядка обладает более крутым спадом АЧХ в пограничной области (при переходе от полосы пропускания к полосе задержания).
3) Эллиптический фильтр (фильтр Кауэра, фильтр Золотарева) имеют частотную характеристику, которая описывается функцией
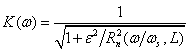 ,
,
где ε и L– параметры, определяющие величину пульсаций АЧХ в полосах пропускания и задержания;
Rn(x) – рациональная функция Чебышева n - го порядка.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.