Эллиптический фильтр при заданном порядке обеспечивает максимальную крутизну спада АЧХ в пограничной области в сравнении с другими типами фильтров.
4) Бесселевский фильтр –фильтр, АЧХ которого по форме близка к гауссовой (колоколообразной) кривой, точнее стремится к ней при увеличении порядка фильтра. Замечательным свойством фильтра Бесселя является высокая линейность ФЧХ в полосе пропускания и как следствие малое изменение времени групповой задержки сигнала.
Функции MatLab для расчета порядка фильтра.
[n,Wn] = buttord(Wp,Ws,Rp,Rs,'s') % - фильтр Баттерворта;
[n,Wn] = cheb1ord(Wp,Ws,Rp,Rs,'s') % фильтр Чебышева 1 рода;
[n,Wn] = cheb2ord(Wp,Ws,Rp,Rs,'s') % фильтр Чебышева 2 рода;
[n,Wn] = ellipord(Wp,Ws,Rp,Rs,'s') % фильтр Кауэра.
Эти функции возвращают два параметра:
n – порядок фильтра;
Wn – частота среза фильтра (этот параметр по разному определяется для разных типов фильтров [1, с.148-149).
Смысл параметров Wp,Ws,Rp,Rs поясняется рис.1.
Расчет нулей и полюсов передаточной функции фильтра-прототипа (вектора z и p) выполняется с помощью следующих функций MatLab:
[z,p,k] = besselap(n) % фильтр
[z,p,k] = buttap(n) % фильтр Баттерворта;
[z,p,k] = cheb1ap(n,Rp) % фильтр Чебышева 1 рода;
[z,p,k] = cheb2ap(n,Rs) % фильтр Чебышева 2 рода;
[z,p,k] = ellipap(n,Rp,Rs) % фильтр Кауэра.
Для вычисления коэффициентов числителя и знаменателя передаточной функции фильтра прототипа (векторы a и b) используется функция
[b,a] = zp2tf(z,p,k).
Функция возвращает векторы a и b – коэффициенты полиномов знаменателя и числителя передаточной функции ФНЧ-прототипа.
Переход от ФНЧ-прототипа к требуемому типу фильтра осуществляется с помощью функций
[bt,at] = lp2lp(b,a,Wс) % ФНЧ – ФНЧ;
[bt,at] = lp2hp(b,a,Wс ) % ФНЧ – ФВЧ;
[bt,at] = lp2bp(b,a,Wo,Bw) % ФНЧ – ПФ;
[bt,at] = lp2bs(b,a,Wo,Bw) % ФНЧ – РФ;
Здесь Wc, рад/с – частота среза (граница полосы пропускания по уровню –3 дБ);
Wo – среднегеометрическое значение границ полосы пропускания;
![]() , где Wв и Wн – верхняя и нижняя границы полосы пропускания фильтра;
, где Wв и Wн – верхняя и нижняя границы полосы пропускания фильтра;
Для расчета частотных характеристик фильтра можно применить функцию MatLab freqs(b,a), которая возвращает значения комплексного коэффициента передачи h, задаваемого векторами a и b на сетке частот, задаваемой вектором w.
h = freqs(b,a,w)
[h,w] = freqs(b,a)
[h,w] = freqs(b,a,f)
Пример расчета режекторного фильтра Чебышева 1 рода с границами полосы пропускания от 5кГц до 8кГц и параметрами ε=0,5, Rs=30дБ.
Fp=3e3; Fs=4e3; eps=0.5;
Wp=2*pi*Fp; Ws=2*pi*Fs;
Rp=10*log10 (1+eps^2); Rs=30;
[n,Wp] = cheb1ord (Wp,Ws,Rp,Rs,'s');
[z,p,k]=cheb1ap (n,Rs);
[b,a]=zp2tf (z,p,k);
f1=5e3; f2=8e3;
w1=2*pi*f1; w2=2*pi*f2;
[b1,a1]=lp2bs (b,a,sqrt (w1*w2), (w2-w1));
f=0:1:14e3;
h=freqs(b2,a2,2*pi*f);
plot(f/1000, abs(h1)), grid, xlabel('f,kHz');
АЧХ фильтра приведена на рис.2.
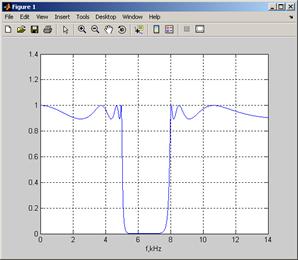
Рис. 2
Пример расчета полосового фильтра Чебышева 1 рода с границами полосы пропускания от 5кГц до 8кГц и параметрами ε=0,5, Rs=30дБ.
Fp=3e3; Fs=4e3; eps=0.2;
Wp=2*pi*Fp; Ws=2*pi*Fs;
Rp=10*log10(1+eps^2);
Rs=30;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.