Синтез моделей фильтров, страница 2

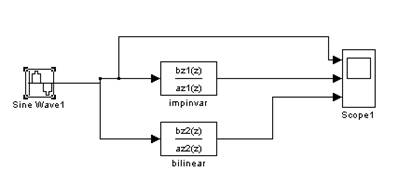
Рис. 4

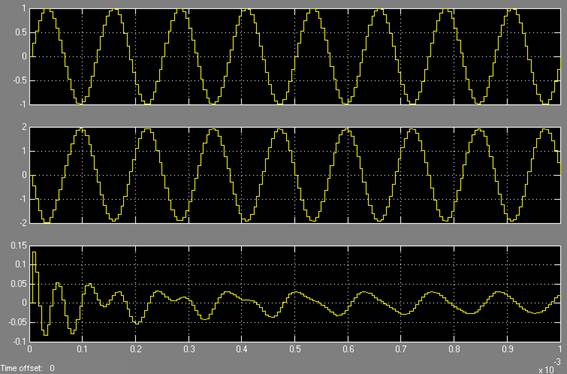
Рис. 5. Сигнал с частотой 8 кГц (верхний график) проходит через дискретные фильтры.

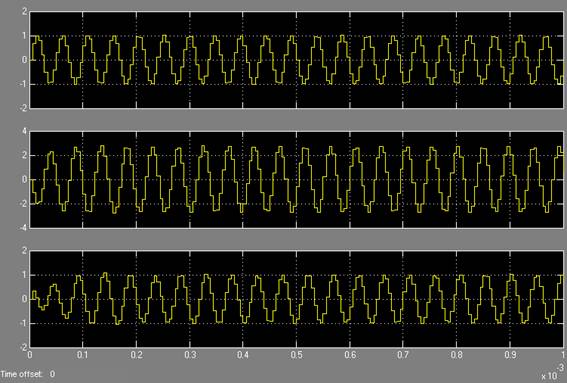
Рис. 6. Сигнал с частотой 21 кГц (верхний график) проходит через дискретные фильтры.

Фильтрация сигнала

%эллиптический фильтр ВЧ

F0=180e3;                         

Fd=180e3;                          %частота дискретизации

Fp=16e3; Fs=14e3;

Wp=Fp/F0; Ws=Fs/F0;               %границы полос пропускания и задерживания (нормированные к частоте Найквиста)

Rp=1; Rs=30;                    %уровни пульсации в полосе пропускания и заграждения

[n,wc]=ellipord(Wp,Ws,Rp,Rs,'s'); %расчет порядка фильтра и частоты среза фильтра

[z,p,k]=ellipap(n,Rp,Rs);         %расчет нулей и полюсов

[b,a]=zp2tf(z,p,k);               %вычисление коэф-тов числителя и знаменателя передаточной функции фильтра-прототипа

Wc=wc*F0*2*pi;                    %частота среза в рад/с

[bt,at]=lp2hp(b,a,Wc);            %коэф-ты аналогового фильтра

[bz,az]=bilinear(bt,at,Fd);       % цифровой фильтр – билинейн. преобр.

[sos, g]=tf2sos(bz,az,'down','two');

t=0:0.001:0.2; % формирование вектора времени

x=rectpuls(t-0.1,0.05); % формирование прямоугольного импульса

b1=sos(1,1:3); a1=sos(1,4:6);% выделение векторов b и a из матрицы sos -1секция

b2=sos(2,1:3); a2=sos(2,4:6);% выделение векторов b и a из матрицы sos -2секция

b3=sos(3,1:3); a3=sos(3,4:6);% выделение векторов b и a из матрицы sos -3секция

y1=filter(b1,a1,x);% фильтрация сигнала в первой секции

y2=g*filter(b2,a2,y1);% фильтрация сигнала во второй секции

y3=filter(b3,a3,y2);% фильтрация сигнала во второй секции

plot(t,x)

hold on

plot(t,y3,':')

grid

hold off

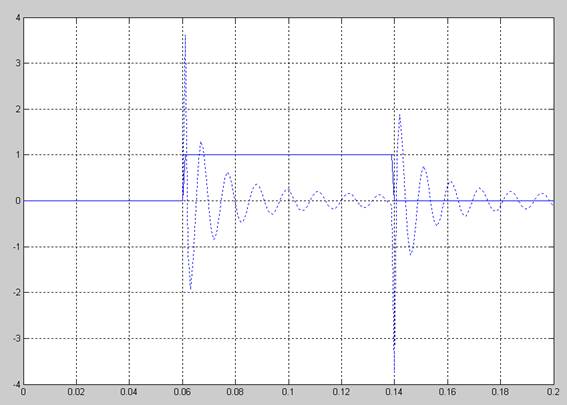
Рис. 7. Прохождение прямоугольного импульса длительностью 0,08 с через 3 секции второго порядка.

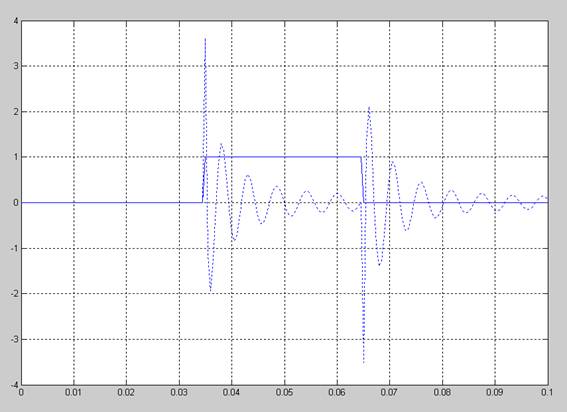
Рис. 8. Прохождение прямоугольного импульса длительностью 0,03 с через 3 секции второго порядка.