|
Ав*,о.е. |
1 |
0,8 |
0,9 |
1 |
1,1 |
1,2 |
1,3 |
|||||
|
Ан*,о.е. |
0,8 |
0,9 |
1 |
1,1 |
1,2 |
1,3 |
1 |
|||||
|
пп*,о.е. |
0,928 |
0,966 |
1 |
1,032 |
1,063 |
1,091 |
0,862 |
0,932 |
1 |
1,066 |
1,129 |
1,191 |
|
Зэ*,о.е. |
1,160 |
1,073 |
1 |
0,938 |
0,885 |
0,839 |
0,862 |
0,932 |
1 |
1,066 |
1,129 |
1,191 |
Исходя из таблицы 1.2 построим прямые чувствительности:
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() nnэ*, о.е.
1.2
1.1
1
0.9
0.8
0.7
0.75 0.8 0.85 0.9 0.95 1 1.05 1.1 1.15 1.2 1.25 1.3 А*, о.е
nnэ*, о.е.
1.2
1.1
1
0.9
0.8
0.7
0.75 0.8 0.85 0.9 0.95 1 1.05 1.1 1.15 1.2 1.25 1.3 А*, о.е
Рис. 1.3.а. Кривые чувствительности обобщенных констант к опт. параметру



![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Зэ*, о.е.
1.2
1.1
1
0.9
0.8
0.7
0.75 0.8 0.85 0.9 0.95 1 1.05 1.1 1.15 1.2 1.25 1.3 А*, о.е
Зэ*, о.е.
1.2
1.1
1
0.9
0.8
0.7
0.75 0.8 0.85 0.9 0.95 1 1.05 1.1 1.15 1.2 1.25 1.3 А*, о.е
Рис. 1.3.б. Кривые чувствительности обобщенных констант к затратам
Как видно из рис 1.3, что изменения исходных данных на стороне ВН повлечет значительные изменения величины оптимизируемого параметра, т.е. модель является чувствительной к параметрам по стороне 10 кВ. Менее чувствительна она к изменению относительной обобщенной константы по цеховым сетям. Влияние же относительных констант на затраты одинаково в то плане, что ведут к незначительным изменениям по конечным относительным затратам.
Следует отметить, что анализируя графики можно определить степень влияния погрешности исходных данных. Так например исходя из рис. 1.3.а можно сказать, что на этапе оптимизации точность (достоверность) исходных данных на стороне 10 кВ должна быть достаточно велика, потому, как есть значительное влияние на определение значений оптимального экономического варианта.
Для решения пятой задачи технико-экономического анализа используется критериальное уравнение (1.35),а у нас один оптимизируемый параметр и на него не накладываются ограничения.
В заключение данной главы определим экономический вариант, т.е. оптимальные число внутрицеховых ТП и соответствующих затрат. Исходя из (1.8), (1.9) и по (1.13) получаем:
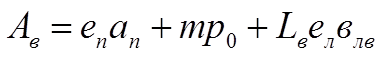 (1.40)
(1.40)
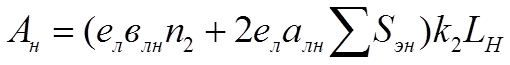 (1.41)
(1.41)
Исходные данные для данных формул взяты из [2]:
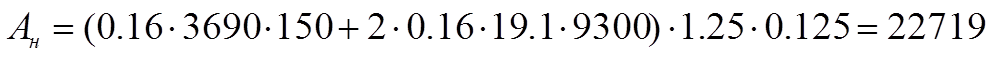
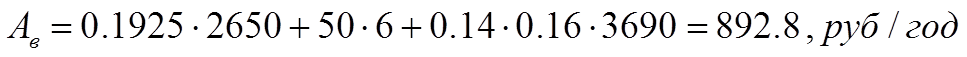
По формулам (1.26.2) и (1.27) получаем:
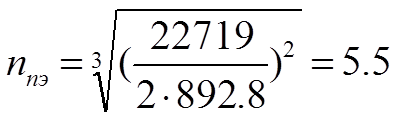
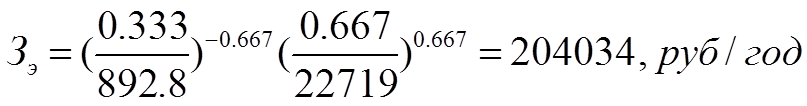
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.